CF1740E Hanging Hearts

Pak Chanek has $ n $ blank heart-shaped cards. Card $ 1 $ is attached directly to the wall while each of the other cards is hanging onto exactly one other card by a piece of string. Specifically, card $ i $ ( $ i > 1 $ ) is hanging onto card $ p_i $ ( $ p_i < i $ ). In the very beginning, Pak Chanek must write one integer number on each card. He does this by choosing any permutation $ a $ of $ [1, 2, \dots, n] $ . Then, the number written on card $ i $ is $ a_i $ . After that, Pak Chanek must do the following operation $ n $ times while maintaining a sequence $ s $ (which is initially empty): 1. Choose a card $ x $ such that no other cards are hanging onto it. 2. Append the number written on card $ x $ to the end of $ s $ . 3. If $ x \neq 1 $ and the number on card $ p_x $ is larger than the number on card $ x $ , replace the number on card $ p_x $ with the number on card $ x $ . 4. Remove card $ x $ . After that, Pak Chanek will have a sequence $ s $ with $ n $ elements. What is the maximum length of the longest non-decreasing subsequence $ ^\dagger $ of $ s $ at the end if Pak Chanek does all the steps optimally? $ ^\dagger $ A sequence $ b $ is a subsequence of a sequence $ c $ if $ b $ can be obtained from $ c $ by deletion of several (possibly, zero or all) elements. For example, $ [3,1] $ is a subsequence of $ [3,2,1] $ , $ [4,3,1] $ and $ [3,1] $ , but not $ [1,3,3,7] $ and $ [3,10,4] $ .

The first line contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of heart-shaped cards. The second line contains $ n - 1 $ integers $ p_2, p_3, \dots, p_n $ ( $ 1 \le p_i < i $ ) describing which card that each card hangs onto.

Print a single integer — the maximum length of the longest non-decreasing subsequence of $ s $ at the end if Pak Chanek does all the steps optimally.

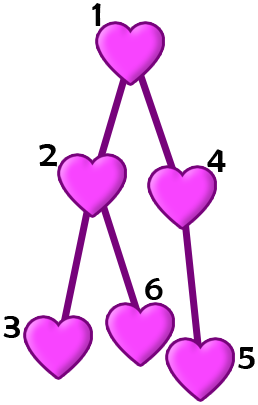
The following is the structure of the cards in the first example.  Pak Chanek can choose the permutation $ a = [1, 5, 4, 3, 2, 6] $ .  Let $ w_i $ be the number written on card $ i $ . Initially, $ w_i = a_i $ . Pak Chanek can do the following operations in order: 1. Select card $ 5 $ . Append $ w_5 = 2 $ to the end of $ s $ . As $ w_4 > w_5 $ , the value of $ w_4 $ becomes $ 2 $ . Remove card $ 5 $ . After this operation, $ s = [2] $ . 2. Select card $ 6 $ . Append $ w_6 = 6 $ to the end of $ s $ . As $ w_2 \leq w_6 $ , the value of $ w_2 $ is left unchanged. Remove card $ 6 $ . After this operation, $ s = [2, 6] $ . 3. Select card $ 4 $ . Append $ w_4 = 2 $ to the end of $ s $ . As $ w_1 \leq w_4 $ , the value of $ w_1 $ is left unchanged. Remove card $ 4 $ . After this operation, $ s = [2, 6, 2] $ . 4. Select card $ 3 $ . Append $ w_3 = 4 $ to the end of $ s $ . As $ w_2 > w_3 $ , the value of $ w_2 $ becomes $ 4 $ . Remove card $ 3 $ . After this operation, $ s = [2, 6, 2, 4] $ . 5. Select card $ 2 $ . Append $ w_2 = 4 $ to the end of $ s $ . As $ w_1 \leq w_2 $ , the value of $ w_1 $ is left unchanged. Remove card $ 2 $ . After this operation, $ s = [2, 6, 2, 4, 4] $ . 6. Select card $ 1 $ . Append $ w_1 = 1 $ to the end of $ s $ . Remove card $ 1 $ . After this operation, $ s = [2, 6, 2, 4, 4, 1] $ . One of the longest non-decreasing subsequences of $ s = [2, 6, 2, 4, 4, 1] $ is $ [2, 2, 4, 4] $ . Thus, the length of the longest non-decreasing subsequence of $ s $ is $ 4 $ . It can be proven that this is indeed the maximum possible length.