CF1740G Dangerous Laser Power

Pak Chanek 有一个 $n \times m$ 的传送门网格。第 $i$ 行第 $j$ 列的传送门记作 $(i,j)$。传送门 $(1,1)$ 和 $(n,m)$ 分别位于网格的西北角和东南角。 每个传送门 $(i,j)$ 有两个设置： - 类型 $t_{i,j}$，取值为 $0$ 或 $1$。 - 强度 $s_{i,j}$，是一个在 $1$ 到 $10^9$ 之间的整数。 每个传送门有 $4$ 个面，分别用整数 $0,1,2,3$ 标记，分别对应北、东、南、西方向。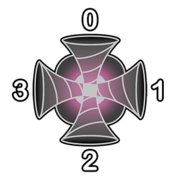当激光以速度 $x_\text{in}$ 从第 $k$ 号面进入传送门 $(i,j)$ 时，它会从第 $(k+2+t_{i,j}) \bmod 4$ 号面离开，离开时的速度为 $x_\text{out} = \max(x_\text{in}, s_{i,j})$。传送门消耗的能量为 $x_\text{out} - x_\text{in}$。 Pak Chanek 今天很无聊。他会以初速度 $1$ 向每个传送门的每个面各发射一束激光，总共 $4nm$ 束。每束激光会在这个传送门网格中穿梭，直到它离开网格或者已经穿过 $10^{100}$ 个传送门。 最后，Pak Chanek 认为一个传送门是“好”的，当且仅当该传送门消耗的总能量对 $2$ 取模等于它的类型。给定所有传送门的强度设置，请为每个传送门分配类型设置，使得“好”的传送门数量最大。

第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 1000$），表示网格的行数和列数。 接下来的 $n$ 行，每行包含 $m$ 个整数，第 $j$ 个整数为 $s_{i,j}$（$1 \leq s_{i,j} \leq 10^9$），表示传送门 $(i,j)$ 的强度。

输出 $n$ 行，每行包含一个长度为 $m$ 的仅由 $0$ 和 $1$ 组成的字符串，表示每个传送门的类型设置。第 $i$ 行第 $j$ 个字符为传送门 $(i,j)$ 的类型设置。 如果有多组解，输出任意一组均可。

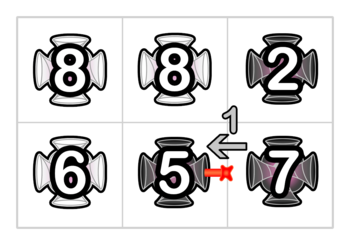
在第一个样例中，考虑 Pak Chanek 向传送门 $(2,2)$ 的第 $1$ 号面发射的激光。激光的运动过程如下： 1. 激光以速度 $1$ 从 $(2,2)$ 的第 $1$ 号面进入，以速度 $5$ 从第 $3$ 号面离开。$(2,2)$ 传送门消耗 $4$ 单位能量。 2. 激光以速度 $5$ 从 $(2,1)$ 的第 $1$ 号面进入，以速度 $6$ 从第 $0$ 号面离开。$(2,1)$ 传送门消耗 $1$ 单位能量。 3. 激光以速度 $6$ 从 $(1,1)$ 的第 $2$ 号面进入，以速度 $8$ 从第 $1$ 号面离开。$(1,1)$ 传送门消耗 $2$ 单位能量。 4. 激光以速度 $8$ 从 $(1,2)$ 的第 $3$ 号面进入，以速度 $8$ 从第 $2$ 号面离开。$(1,2)$ 传送门消耗 $0$ 单位能量。 5. 激光以速度 $8$ 从 $(2,2)$ 的第 $0$ 号面进入，以速度 $8$ 从第 $2$ 号面离开。$(2,2)$ 传送门消耗 $0$ 单位能量。 上述激光运动过程如下图所示。 例如，考虑传送门 $(2,3)$。可以计算出该传送门最终消耗的总能量为 $32$。由于 $32 \bmod 2 = 0$ 且 $t_{2,3} = 0$，因此它是一个“好”的传送门。 由 ChatGPT 4.1 翻译