CF1740H MEX Tree Manipulation

给定一棵有根树，定义树中顶点 $u$ 的值为其所有子节点的值的 MEX $^\dagger$。注意，这里只考虑子节点，而不是所有后代。特别地，叶子的值为 $0$。 Pak Chanek 有一棵初始只包含编号为 $1$ 的根节点的有根树。Pak Chanek 将进行 $q$ 次操作。在第 $i$ 次操作中，Pak Chanek 会得到一个整数 $x_i$。Pak Chanek 需要将编号为 $i+1$ 的新顶点作为顶点 $x_i$ 的子节点加入树中。每次加入新顶点后，Pak Chanek 需要重新计算所有顶点的值，并输出当前树中所有顶点的值之和。 $^\dagger$ MEX（minimum excluded）指的是一个数组中未出现的最小非负整数。例如，$[0,1,1,2,6,7]$ 的 MEX 是 $3$，$[6,9]$ 的 MEX 是 $0$。

第一行包含一个整数 $q$（$1 \leq q \leq 3 \cdot 10^5$），表示操作次数。 接下来的 $q$ 行，每行包含一个整数 $x_i$（$1 \leq x_i \leq i$），表示第 $i$ 次操作的描述。

对于每次操作，输出一行一个整数，表示加入新顶点后当前树中所有顶点的值之和。

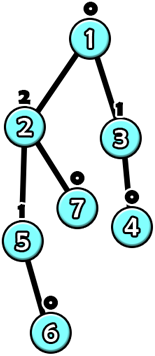
在第一个样例中，第 $6$ 次操作后树的结构如下图所示。  - 顶点 $7$ 是叶子，所以它的值为 $0$。 - 顶点 $6$ 是叶子，所以它的值为 $0$。 - 顶点 $5$ 只有一个值为 $0$ 的子节点，所以它的值为 $1$。 - 顶点 $4$ 是叶子，所以它的值为 $0$。 - 顶点 $3$ 只有一个值为 $0$ 的子节点，所以它的值为 $1$。 - 顶点 $2$ 有两个子节点，值分别为 $0$ 和 $1$，所以它的值为 $2$。 - 顶点 $1$ 有两个子节点，值分别为 $1$ 和 $2$，所以它的值为 $0$。 所有顶点的值之和为 $0+0+1+0+1+2+0=4$。 由 ChatGPT 4.1 翻译