CF1740H MEX Tree Manipulation

Given a rooted tree, define the value of vertex $ u $ in the tree recursively as the MEX $ ^\dagger $ of the values of its children. Note that it is only the children, not all of its descendants. In particular, the value of a leaf is $ 0 $ . Pak Chanek has a rooted tree that initially only contains a single vertex with index $ 1 $ , which is the root. Pak Chanek is going to do $ q $ queries. In the $ i $ -th query, Pak Chanek is given an integer $ x_i $ . Pak Chanek needs to add a new vertex with index $ i+1 $ as the child of vertex $ x_i $ . After adding the new vertex, Pak Chanek needs to recalculate the values of all vertices and report the sum of the values of all vertices in the current tree. $ ^\dagger $ The MEX (minimum excluded) of an array is the smallest non-negative integer that does not belong to the array. For example, the MEX of $ [0,1,1,2,6,7] $ is $ 3 $ and the MEX of $ [6,9] $ is $ 0 $ .

The first line contains a single integer $ q $ ( $ 1 \le q \le 3 \cdot 10^5 $ ) — the number of operations. Each of the next $ q $ lines contains a single integer $ x_i $ ( $ 1 \leq x_i \leq i $ ) — the description of the $ i $ -th query.

For each query, print a line containing an integer representing the sum of the new values of all vertices in the tree after adding the vertex.

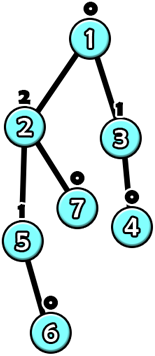
In the first example, the tree after the $ 6 $ -th query will look like this.  - Vertex $ 7 $ is a leaf, so its value is $ 0 $ . - Vertex $ 6 $ is a leaf, so its value is $ 0 $ . - Vertex $ 5 $ only has a child with value $ 0 $ , so its value is $ 1 $ . - Vertex $ 4 $ is a leaf, so its value is $ 0 $ . - Vertex $ 3 $ only has a child with value $ 0 $ , so its value is $ 1 $ . - Vertex $ 2 $ has children with values $ 0 $ and $ 1 $ , so its value is $ 2 $ . - Vertex $ 1 $ has children with values $ 1 $ and $ 2 $ , so its value is $ 0 $ . The sum of the values of all vertices is $ 0+0+1+0+1+2+0=4 $ .