CF1741F Multi-Colored Segments

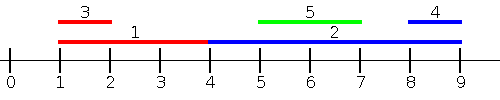
Dmitry 在坐标轴 $Ox$ 上有 $n$ 条不同颜色的线段。每条线段由三个整数 $l_i$、$r_i$ 和 $c_i$ 描述（$1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$），其中 $l_i$ 和 $r_i$ 分别表示第 $i$ 条线段的两个端点的坐标，$c_i$ 表示该线段的颜色。 Dmitry 喜欢寻找线段之间的最小距离。但他认为同色线段之间的配对没有意思。因此，他想知道对于每一条线段，到最近的不同颜色的线段的距离是多少。 两条线段之间的距离定义为：第一条线段上的某个点与第二条线段上的某个点之间距离的最小值。特别地，如果两条线段相交，则它们之间的距离为 $0$。 例如，Dmitry 有 $5$ 条线段：  - 第一条线段与第二条线段相交（且颜色不同），所以它们的答案都是 $0$。 - 对于第 $3$ 条线段，最近的不同颜色线段是第 $2$ 条，与其的距离为 $2$。 - 对于第 $4$ 条线段，最近的不同颜色线段是第 $5$ 条，与其的距离为 $1$。 - 第 $5$ 条线段完全位于第 $2$ 条线段内部（且颜色不同），所以它们的答案都是 $0$。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 2 \cdot 10^5$），表示线段的数量。 接下来的 $n$ 行，每行包含三个整数 $l_i$、$r_i$ 和 $c_i$（$1 \le l_i \le r_i \le 10^9, 1 \le c_i \le n$），分别表示第 $i$ 条线段的左端点、右端点和颜色。保证至少有 $2$ 条线段颜色不同。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一行 $n$ 个整数，第 $i$ 个数表示第 $i$ 条线段到最近的不同颜色线段的距离。

在第一个样例的第一个测试用例中，只有一条颜色为 $2$ 的线段，其他线段颜色为 $1$。因此，对于颜色为 $1$ 的线段，答案等于到第 $3$ 条线段的距离；对于第 $3$ 条线段，答案等于到颜色为 $1$ 的线段的最小距离。 在第一个样例的第二个测试用例中，只有 $2$ 条线段，对于它们来说，答案等于它们之间的距离。 在第一个样例的第三个测试用例中，每条线段的至少一个端点与不同颜色的线段相交，所以所有答案都是 $0$。 第一个样例的第四个测试用例在题目描述中已经给出。 在第一个样例的第五个测试用例中，一条线段完全包含在另一条线段内部，对于它们来说，答案都是 $0$。 在第一个样例的第六个测试用例中，所有线段都是不同颜色的点。 由 ChatGPT 4.1 翻译