CF1741G Kirill and Company

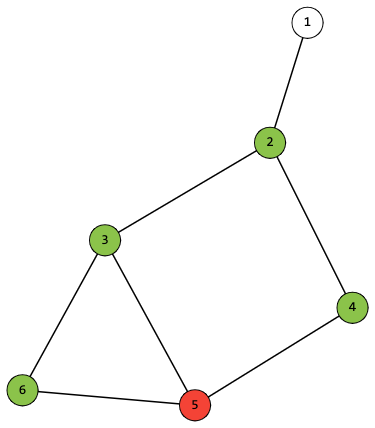
Kirill 住在一个有 $n$ 个顶点和 $m$ 条边的连通无向图的顶点 $1$ 上。一天傍晚，他召集了 $f$ 个朋友，第 $i$ 个朋友住在顶点 $h_i$。现在所有朋友都在顶点 $1$，第 $i$ 个朋友需要回到他自己的家 $h_i$。 傍晚即将结束，大家要离开了。结果发现有 $k$ 个（$k \le 6$）朋友没有车，如果没人载他们，他们就得步行回家。有车的朋友可以载任意数量没有车的朋友，但前提是他能在前往自己家的某条最短路径上顺路送他们回家。 例如，在下图中，住在顶点 $h_i=5$ 的朋友可以顺路送住在以下顶点集合的朋友：$[2, 3]$，$[2, 4]$，$[2]$，$[3]$，$[4]$，但不能顺路送住在顶点 $6$ 的朋友，也不能同时送 $[3, 4]$。  图中绿色顶点表示没有车的朋友，红色顶点表示有车的朋友。Kirill 希望让尽可能少的朋友不得不步行。请你帮他计算最少需要步行的朋友人数。

输入的第一行为一个整数 $t$（$1 \le t \le 10^3$），表示测试用例的数量。 每个测试用例的第一行为两个整数 $n$ 和 $m$（$2 \le n \le 10^4$，$n-1 \le m \le \min(10^4, \frac{n \cdot (n-1)}{2})$），分别表示顶点数和边数。 接下来的 $m$ 行，每行两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \ne v$），表示一条连接顶点 $u$ 和 $v$ 的边。保证任意一对顶点之间至多有一条边（即无重边）。 然后一行一个整数 $f$（$1 \le f \le 10^4$），表示 Kirill 的朋友数。 接下来一行 $f$ 个整数 $h_1, h_2, \dots, h_f$（$2 \le h_i \le n$），表示每个朋友的家所在的顶点。顶点可以重复。 然后一行一个整数 $k$（$1 \le k \le \min(6, f)$），表示没有车的朋友数。 最后一行 $k$ 个整数 $p_1, p_2, \dots, p_k$（$1 \le p_i \le f$，$p_i < p_{i+1}$），表示没有车的朋友在 $h$ 数组中的下标。 保证所有测试用例中 $n$、$m$、$f$ 的总和不超过 $10^4$。

输出 $t$ 行，每行一个整数，表示对应测试用例中最少需要步行的朋友人数。

第一个样例的第一个测试用例已在题目描述中解释。 第一个样例的第二个测试用例中，有两个有车的朋友住在顶点 $5$，其中一个可以顺路送住在顶点 $2$ 和 $3$ 的朋友，另一个可以送住在顶点 $4$ 的朋友，只有住在顶点 $6$ 的朋友需要步行。 由 ChatGPT 4.1 翻译