The Beach

## 题目大意 有一个 $n\times m$ 的网格图，场地上有许多不可移动的障碍，标记为 `#`，还有一些可以移动的障碍，如果他是横着的，定义它的一边为 `L`，另一边为 `R`；否则定义它的上边为 `U`，下边为 `D`，现在需要在这个网格图中空出一个 $1\times 2$ 的空位，可以移动的障碍移动如下： - 选择固定它的一边，将其旋转 $90^\degree$，花费 $p$ 单位，前提是旋转后不准与其他障碍重合。 - 将其平移一个单位，花费 $q$ 单位，前提是平移后不准与其他障碍重合。 现在要求出在这个网格图里空出 $1\times 2$ 的空位，至少需要花费多少单位，如果不可能，输出 `-1`。 ## 输入格式 第一行两个整数 $1\leqslant n,m\leqslant 3\times 10^5,n\times m\leqslant 3\times 10^5$，表示这个网格的大小。 第二行两个整数 $1\leqslant p,q\leqslant 10^9$，如题意所述。 接下来 $n$ 行，每行 $m$ 个字符，每个字符为 `.`（表示空位）、`#`（表示不可移动障碍）、`L`、`R`、`U`、`D`（分别表示可移动的障碍是如何摆放的）中的一种。 ## 输出格式 输出一个整数表示最小花费，如果不存在这样的方案，输出 `-1`。 ## 样例解释 第一个样例中可以把位于 $(1,2),(1,3)$ 的障碍往左移动一格，$(2,3),(2,4)$ 的障碍往右移动一格，花费 $2q=4$。 第二个样例中无论如何移动障碍都不可能空出 $1\times 2$ 的空位，输出 `-1`。

Andrew loves the sea. That's why, at the height of the summer season, he decided to go to the beach, taking a sunbed with him to sunbathe. The beach is a rectangular field with $ n $ rows and $ m $ columns. Some cells of the beach are free, some have roads, stones, shops and other non-movable objects. Some of two adjacent along the side cells can have sunbeds located either horizontally or vertically. Andrew hopes to put his sunbed somewhere, but that's a bad luck, there may no longer be free places for him! That's why Andrew asked you to help him to find a free place for his sunbed. Andrew's sunbed also should be places on two adjacent cells. If there are no two adjacent free cells, then in order to free some place for a sunbed, you will have to disturb other tourists. You can do the following actions: - Come to some sunbed and, after causing $ p $ units of discomfort to its owner, lift the sunbed by one of its sides and rotate it by $ 90 $ degrees. One half of the sunbed must remain in the same cell and another half of the sunbed must move to the free cell. At the same time, anything could be on the way of a sunbed during the rotation . Rotation of the sunbed by $ 90 $ degrees around cell $ (1, 2) $ . - Come to some sunbed and, after causing $ q $ units of discomfort to its owner, shift the sunbed along its long side by one cell. One half of the sunbed must move to the place of another, and another — to the free cell. Shift of the sunbed by one cell to the right. In any moment each sunbed occupies two adjacent free cells. You cannot move more than one sunbed at a time. Help Andrew to free a space for his sunbed, causing the minimum possible number of units of discomfort to other tourists, or detect that it is impossible.

The first line contains two integers $ n $ and $ m $ ( $ 1 \le n, m \le 300\,000 $ , $ 1 \le n \cdot m \le 300\,000 $ ) — the number of rows and columns in rectangle. The second line contains two integers $ p $ and $ q $ ( $ 1 \le p, q \le 10^9 $ ) — the number of units of discomfort caused by rotation and shift of a sunbed, respectively. Each of the following $ n $ lines contains $ m $ characters, describing cells of the rectangle. Each lines consists of characters "L", "R", "D", "U", "." and "\#", denoting the type of the cell. Characters "L", "R", "D" and "U" denote a half of a sunbed placed in the cell — left, right, bottom and top half, respectively. Character "." denotes a free cell and character "\#" — a cell, occupied by some non-movable object.

Print one integer — the minimum possible number of units of discomfort, caused to other tourists, to free a space for a sunbed. If it is impossible to free a space for a sunbed, print $ -1 $ .

2 5
5 2
.LR##
##LR.

4

2 3
4 5
LR.
#.#

-1

4 3
10 10
.LR
###
UU#
DD.

-1

3 6
10 7
.U##.#
#DLR##
.##LR.

24

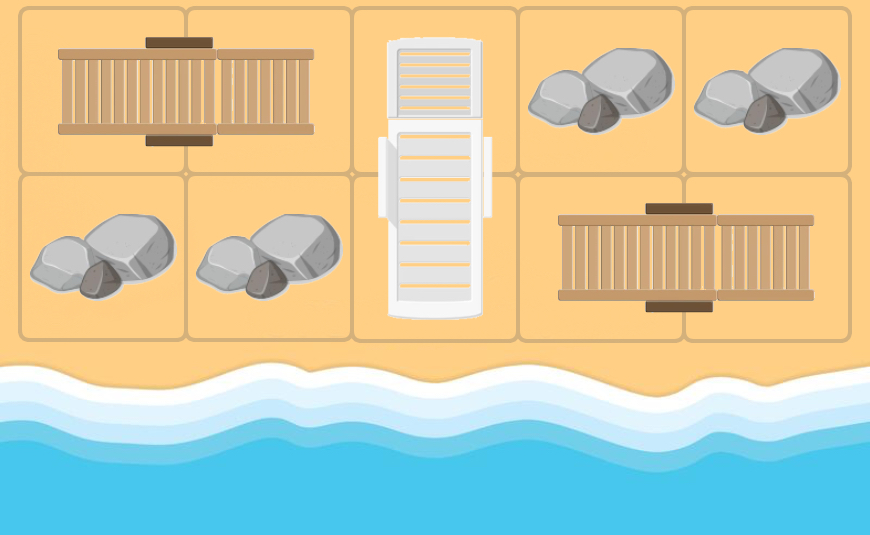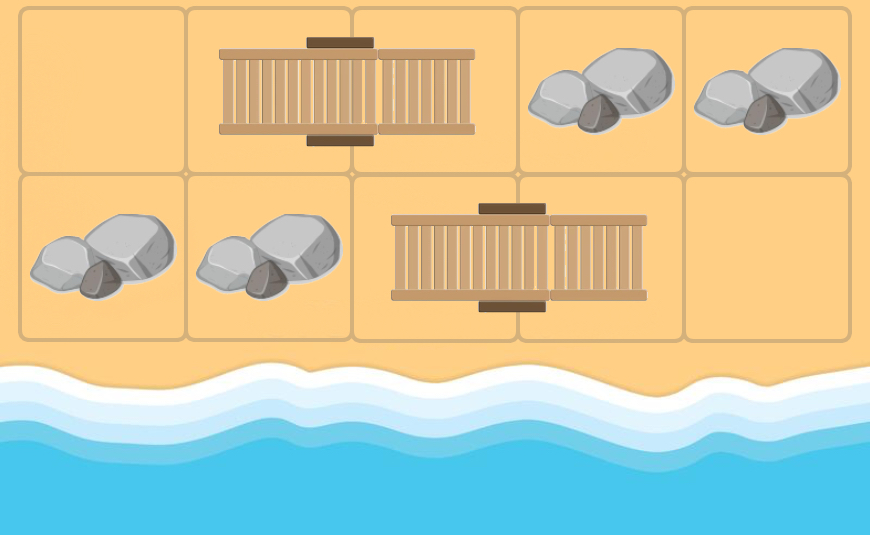In the first example we can shift upper sunbed to the left and lower sunbed — to the right. Andrew will be able to put his sunbed vertically in the middle of the beach. We well cause $ 2 + 2 = 4 $ units of discomfort. It is easy to prove that it is an optimal answer. Optimal strategy in the first example (Andrew's sunbed is colored white). In the second example it is impossible to free a space for Andrew's sunbed. All possible states of the beach after any rotates and shifts are illustrated in the problem statement.