CF1760D Challenging Valleys

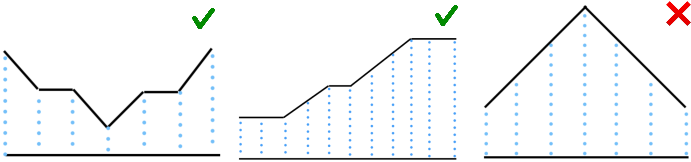You are given an array $ a[0 \dots n-1] $ of $ n $ integers. This array is called a "valley" if there exists exactly one subarray $ a[l \dots r] $ such that: - $ 0 \le l \le r \le n-1 $ , - $ a_l = a_{l+1} = a_{l+2} = \dots = a_r $ , - $ l = 0 $ or $ a_{l-1} > a_{l} $ , - $ r = n-1 $ or $ a_r < a_{r+1} $ . Here are three examples: The first image shows the array \[ $ 3, 2, 2, 1, 2, 2, 3 $ \], it is a valley because only subarray with indices $ l=r=3 $ satisfies the condition. The second image shows the array \[ $ 1, 1, 1, 2, 3, 3, 4, 5, 6, 6, 6 $ \], it is a valley because only subarray with indices $ l=0, r=2 $ satisfies the codition. The third image shows the array \[ $ 1, 2, 3, 4, 3, 2, 1 $ \], it is not a valley because two subarrays $ l=r=0 $ and $ l=r=6 $ that satisfy the condition. You are asked whether the given array is a valley or not. Note that we consider the array to be indexed from $ 0 $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 1 \leq n \leq 2\cdot10^5 $ ) — the length of the array. The second line of each test case contains $ n $ integers $ a_i $ ( $ 1 \leq a_i \leq 10^9 $ ) — the elements of the array. It is guaranteed that the sum of $ n $ over all test cases is smaller than $ 2\cdot10^5 $ .

For each test case, output "YES" (without quotes) if the array is a valley, and "NO" (without quotes) otherwise. You can output the answer in any case (for example, the strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive answer).

The first three test cases are explained in the statement.