CF1763E Node Pairs

我们称有向图中的有序节点对 $(u, v)$ 为“单向对”，当且仅当 $u \neq v$，存在从 $u$ 到 $v$ 的路径，且不存在从 $v$ 到 $u$ 的路径。 如果一个有向图中，恰好存在 $p$ 个有序节点对 $(u, v)$ 满足 $u < v$ 且 $u$ 和 $v$ 互相可达，则称该有向图为 $p$-可达图。请你求出构造一个 $p$-可达图所需的最小节点数。 此外，在所有节点数最少的 $p$-可达图中，记 $G$ 为单向对数量最多的图。请你求出该最大单向对数量。

输入仅一行，包含一个整数 $p$（$0 \le p \le 2 \cdot 10^5$），表示有序节点对的数量。

输出一行两个整数，分别表示构造一个 $p$-可达图所需的最小节点数，以及在所有节点数最少的 $p$-可达图中，单向对的最大数量。

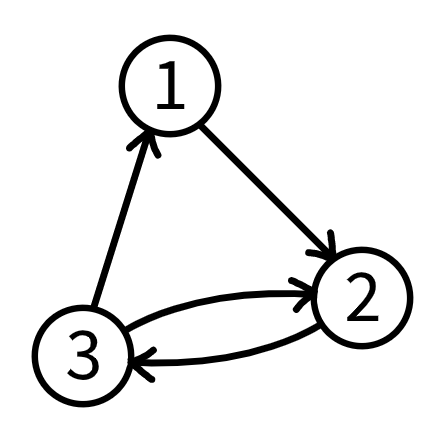
在第一个测试样例中，构造一个 $3$-可达图所需的最小节点数为 $3$。在所有 $3$-可达且节点数为 $3$ 的有向图中，下图 $G$ 是单向对数量最多的图之一，其单向对数量为 $0$。  由 ChatGPT 4.1 翻译