CF1763F Edge Queries

给定一个无向连通图，包含 $n$ 个节点和 $m$ 条边。对于图中的每个节点 $u$，都满足以下条件： - 设 $S_u$ 为从 $u$ 出发并回到 $u$ 的最长简单环所包含的顶点集合。 - 设 $C_u$ 为从 $u$ 出发并回到 $u$ 的所有简单环所包含的顶点集合的并集。 - $S_u = C_u$。 你需要回答 $q$ 个询问。 对于每个询问，给定节点 $a$ 和节点 $b$。在所有从 $a$ 到 $b$ 的简单路径上出现的边中，统计有多少条边满足：如果移除该边，$a$ 和 $b$ 仍然可以互相到达。

第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$1 \le m \le \min(2 \cdot 10^5, \frac{n \cdot (n-1)}{2})$），分别表示节点数和边数。 接下来 $m$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \neq v$），表示节点 $u$ 和节点 $v$ 之间有一条无向边。 保证任意一对顶点之间至多只有一条边，且给定的图是连通的。 接下来一行包含一个整数 $q$（$1 \le q \le 2 \cdot 10^5$），表示询问的数量。 接下来 $q$ 行，每行包含两个整数 $a$ 和 $b$（$1 \le a, b \le n$），表示一次询问。

对于每个询问，输出一个整数，表示该询问的答案。

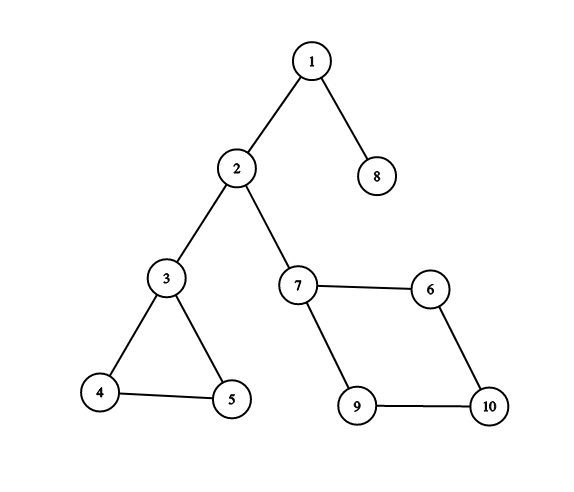
第一个样例中的图如下：  第一个询问是 $(1, 4)$。从 $1$ 到 $4$ 的所有简单路径上共有 $5$ 条边。其中，边 $(3, 4), (4, 5), (5, 3)$ 会被计入该询问的答案。 第四个询问是 $(2, 8)$。从 $2$ 到 $8$ 只有一条简单路径，因此没有边会被计入答案。 第五个询问是 $(7, 10)$。从 $7$ 到 $10$ 的所有简单路径上共有 $4$ 条边，这些边都会被计入答案。 由 ChatGPT 4.1 翻译