CF1764C Doremy's City Construction

哆蕾咪的新城市正在建设中！这座城市可以被看作一个简单无向图，有 $n$ 个顶点。第 $i$ 个顶点的海拔为 $a_i$。现在哆蕾咪正在决定哪些顶点对之间应该连边。 出于经济原因，图中不允许有自环或重边。 出于安全原因，不允许存在互不相同的顶点 $u$、$v$ 和 $w$，使得 $a_u \leq a_v \leq a_w$ 且边 $(u,v)$ 和 $(v,w)$ 都存在。 在这些约束下，哆蕾咪想知道图中最多可以有多少条边。你能帮帮她吗？ 注意，所构造的图可以是不连通的。

输入包含多组测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 2 \cdot 10^5$），表示顶点数。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$1 \leq a_i \leq 10^6$），表示每个顶点的海拔。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出图中最多可以有多少条边。

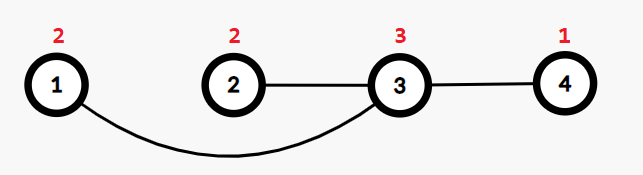
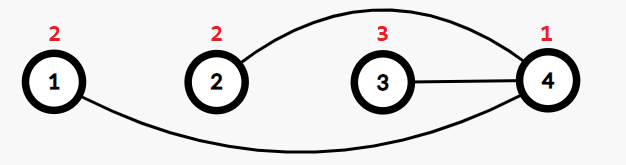
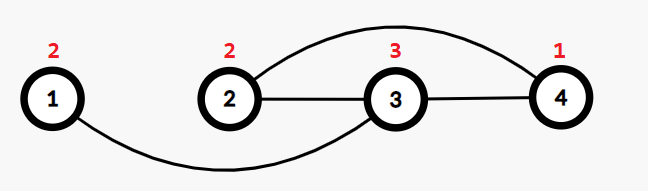
在第一个测试用例中，图中最多只能有 $3$ 条边。一种可能的构造方式是连接 $(1,3)$、$(2,3)$、$(3,4)$。下图中，节点 $i$ 上方的红色数字为 $a_i$。  下列是所有满足条件的 $u$、$v$、$w$，使得边 $(u,v)$ 和 $(v,w)$ 都存在： - $u=1$，$v=3$，$w=2$； - $u=1$，$v=3$，$w=4$； - $u=2$，$v=3$，$w=1$； - $u=2$，$v=3$，$w=4$； - $u=4$，$v=3$，$w=1$； - $u=4$，$v=3$，$w=2$。 另一种可能的构造方式是连接 $(1,4)$、$(2,4)$、$(3,4)$。  一种不合法的构造方式是连接 $(1,3)$、$(2,3)$、$(2,4)$、$(3,4)$。因为当 $u=4$，$v=2$，$w=3$ 时，$a_u \leq a_v \leq a_w$ 成立，且相应的边都存在。  由 ChatGPT 4.1 翻译