CF1764D Doremy's Pegging Game

Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs. Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will: 1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed; 2. remove the red peg $ i $ ; 3. append $ i $ to the back of $ a $ . Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number. 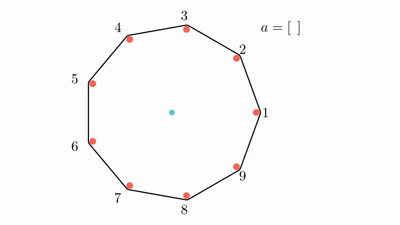 game with $ n=9 $ and $ a=[7,5,2,8,3,9,4] $ and another game with $ n=8 $ and $ a=[3,4,7,1,8,5,2] $

The first line contains two integers $ n $ and $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — the number of red pegs and the modulo respectively. $ p $ is guaranteed to be a prime number.

Output a single integer, the number of different arrays $ a $ that can be produced by the process described above modulo $ p $ .

In the first test case, $ n=4 $ , some possible arrays $ a $ that can be produced are $ [4,2,3] $ and $ [1,4] $ . However, it is not possible for $ a $ to be $ [1] $ or $ [1,4,3] $ .