CF1764D Doremy's Pegging Game

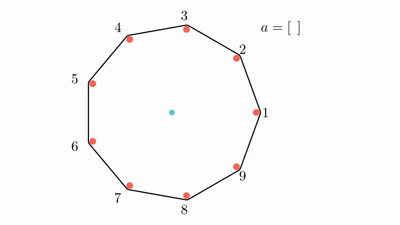
Doremy 有 $n+1$ 个钉子。有 $n$ 个红色钉子，按逆时针顺序编号为 $1$ 到 $n$，它们被排列成一个正 $n$ 边形的顶点。此外，正多边形的中心还有一个直径略小的蓝色钉子。一根橡皮筋被套在所有红色钉子上。 今天 Doremy 很无聊，决定玩一个游戏。她初始有一个空数组 $a$。只要橡皮筋没有碰到蓝色钉子，她就会： 1. 选择一个 $i$（$1 \leq i \leq n$），且红色钉子 $i$ 尚未被移除； 2. 移除红色钉子 $i$； 3. 将 $i$ 添加到数组 $a$ 的末尾。 Doremy 想知道，通过上述过程，可能产生多少种不同的数组 $a$。由于答案可能很大，你只需要输出答案对 $p$ 取模的结果。$p$ 保证是一个质数。  如图，左侧为 $n=9$，$a=[7,5,2,8,3,9,4]$ 的一种情况，右侧为 $n=8$，$a=[3,4,7,1,8,5,2]$ 的另一种情况。

第一行包含两个整数 $n$ 和 $p$（$3 \leq n \leq 5000$，$10^8 \le p \le 10^9$）——红色钉子的数量和取模的质数。 $p$ 保证为质数。

输出一个整数，表示通过上述过程可能产生的不同数组 $a$ 的数量，对 $p$ 取模。

在第一个测试样例中，$n=4$，一些可能的数组 $a$ 包括 $[4,2,3]$ 和 $[1,4]$。但 $a$ 不能为 $[1]$ 或 $[1,4,3]$。 由 ChatGPT 4.1 翻译