CF1764F Doremy's Experimental Tree

Doremy 有一棵带权树，这棵树有 $n$ 个顶点，边权为 $1$ 到 $10^9$ 之间的整数。她在这棵树上进行了 $\frac{n(n+1)}{2}$ 次实验。 在每次实验中，Doremy 选择顶点 $i$ 和 $j$，其中 $j \leq i$，并在它们之间直接连一条权值为 $1$ 的边。此时，图中恰好会出现一个环（当 $i=j$ 时为自环）。Doremy 定义 $f(i,j)$ 为所有顶点到该环的最短路径长度之和。 形式化地，设 $\mathrm{dis}_{i,j}(x,y)$ 表示在加入权值为 $1$ 的边 $(i,j)$ 后，顶点 $x$ 到 $y$ 的最短路径长度，$S_{i,j}$ 表示在加入边 $(i,j)$ 后位于环上的所有顶点的集合。那么， $$ f(i,j)=\sum_{x=1}^{n}\left(\min_{y\in S_{i,j}}\mathrm{dis}_{i,j}(x,y)\right)。 $$ Doremy 记录下了所有 $1 \leq j \leq i \leq n$ 的 $f(i,j)$ 的值，然后去睡觉了。然而，醒来后她发现树不见了。幸运的是，她还保留着 $f(i,j)$ 的值，并且知道每个值对应的 $i$ 和 $j$。现在，给定所有 $f(i,j)$ 的值，你能帮她还原出这棵树吗？ 保证至少存在一棵满足条件的树。

输入的第一行包含一个整数 $n$（$2 \le n \le 2000$），表示树的顶点数。 接下来的 $n$ 行给出一个下三角矩阵，第 $i$ 行包含 $i$ 个整数，第 $i$ 行第 $j$ 个整数为 $f(i,j)$（$0 \le f(i,j) \le 2 \cdot 10^{15}$）。 保证存在一棵边权为 $1$ 到 $10^9$ 的树，使得所有 $f(i,j)$ 与输入一致。

输出 $n-1$ 行，每行三个整数 $u_i$、$v_i$、$w_i$（$1 \le u_i, v_i \le n$，$1 \le w_i \le 10^9$），表示一条连接 $u_i$ 和 $v_i$ 的边，权值为 $w_i$。 如果有多组答案，输出任意一组均可。 所有边必须构成一棵树，并且所有 $f(i,j)$ 的值与输入一致。

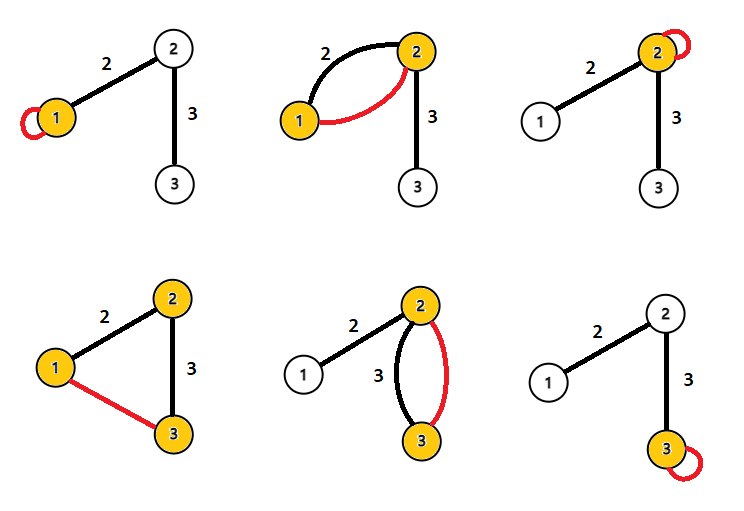
在第一个测试样例中，下图从左到右、从上到下，分别展示了在连接 $(1,1)$、$(1,2)$、$(1,3)$、$(2,2)$、$(2,3)$、$(3,3)$ 时的图。黄色节点表示在环上的节点。  由 ChatGPT 4.1 翻译