CF1764F Doremy's Experimental Tree

Doremy has an edge-weighted tree with $ n $ vertices whose weights are integers between $ 1 $ and $ 10^9 $ . She does $ \frac{n(n+1)}{2} $ experiments on it. In each experiment, Doremy chooses vertices $ i $ and $ j $ such that $ j \leq i $ and connects them directly with an edge with weight $ 1 $ . Then, there is exactly one cycle (or self-loop when $ i=j $ ) in the graph. Doremy defines $ f(i,j) $ as the sum of lengths of shortest paths from every vertex to the cycle. Formally, let $ \mathrm{dis}_{i,j}(x,y) $ be the length of the shortest path between vertex $ x $ and $ y $ when the edge $ (i,j) $ of weight $ 1 $ is added, and $ S_{i,j} $ be the set of vertices that are on the cycle when edge $ (i,j) $ is added. Then, $$ f(i,j)=\sum_{x=1}^{n}\left(\min_{y\in S_{i,j}}\mathrm{dis}_{i,j}(x,y)\right). $$ Doremy writes down all values of $ f(i,j) $ such that $ 1 \leq j \leq i \leq n $ , then goes to sleep. However, after waking up, she finds that the tree has gone missing. Fortunately, the values of $ f(i,j) $ are still in her notebook, and she knows which $ i $ and $ j $ they belong to. Given the values of $ f(i,j)$, can you help her restore the tree? It is guaranteed that at least one suitable tree exists.

The first line of input contains a single integer $ n $ ($ 2 \le n \le 2000 $) — the number of vertices in the tree. The following $ n $ lines contain a lower-triangular matrix with $ i $ integers on the $ i $ -th line; the $ j $ -th integer on the $ i $ -th line is $ f(i,j) $ ( $ 0 \le f(i,j) \le 2\cdot 10^{15} $ ). It is guaranteed that there exists a tree whose weights are integers between $ 1 $ and $ 10^9 $ such that the values of $ f(i,j) $ of the tree match those given in the input.

Print $ n-1 $ lines describing the tree. In the $ i $ -th line of the output, output three integers $ u_i $ , $ v_i $ , $ w_i $ ( $ 1 \le u_i,v_i \le n $ , $ 1 \le w_i \le 10^9 $ ), representing an edge $ (u_i,v_i) $ whose weight is $ w_i $ . If there are multiple answers, you may output any. All edges must form a tree and all values of $ f(i,j) $ must match those given in the input.

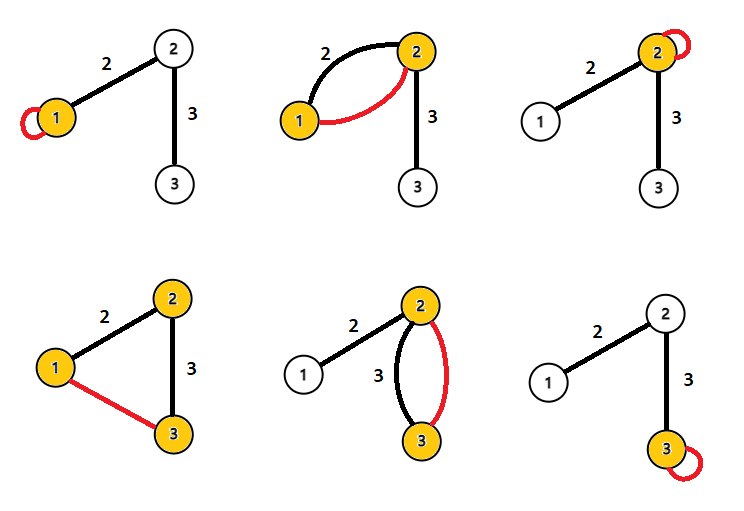
In the first test case, the picture below, from left to right, from top to bottom, shows the graph when pairs $ (1,1) $ , $ (1,2) $ , $ (1,3) $ , $ (2,2) $ , $ (2,3) $ , $ (3,3) $ are connected with an edge, respectively. The nodes colored yellow are on the cycle.