CF1764H Doremy's Paint 2
题目描述
Doremy 有 $n$ 个油漆桶,用一个长度为 $n$ 的数组 $a$ 表示。第 $i$ 个桶中油漆的颜色为 $a_i$。初始时,$a_i = i$。
Doremy 有 $m$ 个区间 $[l_i, r_i]$($1 \le l_i \le r_i \le n$)。每个区间描述一次操作。第 $i$ 次操作如下:
- 对于所有满足 $l_i < j \leq r_i$ 的 $j$,将 $a_j$ 赋值为 $a_{l_i}$。
Doremy 还会选择一个整数 $k$。她想知道,对于每个 $x$ 从 $0$ 到 $m-1$,在从初始数组出发,依次执行操作 $x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1$ 后,数组中有多少种不同的颜色。你能帮她计算这些值吗?注意,对于每个 $x$,都要从初始数组重新开始,仅执行这 $k$ 次指定顺序的操作。
输入格式
输入的第一行包含三个整数 $n$、$m$ 和 $k$($1 \le n, m \le 2 \cdot 10^5$,$1 \le k \le m$)——数组 $a$ 的长度、操作的总数,以及 Doremy 选择的整数。
接下来的 $m$ 行中,第 $i$ 行包含两个整数 $l_i$ 和 $r_i$($1 \le l_i \le r_i \le n$)——第 $i$ 个操作对应的区间。
输出格式
输出 $m$ 个整数。第 $(x+1)$ 个整数表示:如果从初始数组出发,依次执行操作 $x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1$ 后,数组中不同颜色的数量。
说明/提示
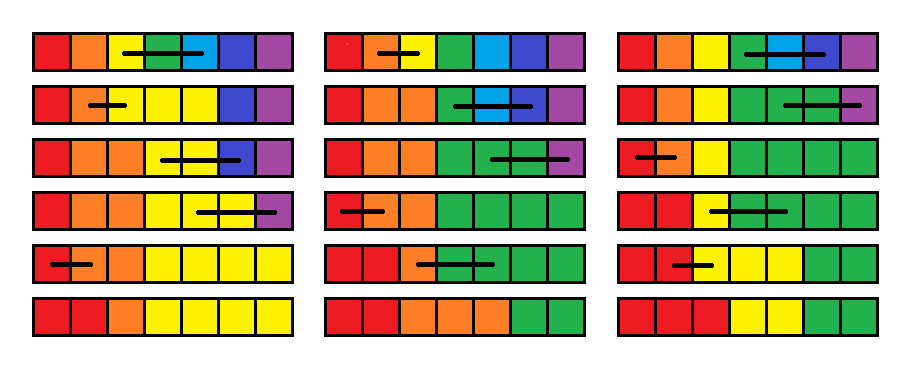
在第一个测试用例中,下图展示了 $x=0,1,2$ 时最终数组的情况。
由 ChatGPT 4.1 翻译