CF1765I Infinite Chess

黑王生活在一个拥有无限多列（文件）和 $8$ 行（排）的棋盘上。列用所有整数编号（包括负数）。行从 $1$ 到 $8$ 编号。 最初，黑王位于起始格子 $(x_s, y_s)$，他需要到达目标格子 $(x_t, y_t)$。不幸的是，棋盘上还有白棋子，它们威胁着黑王。经过协商，白棋同意让黑王在以下条件下前往目标格子： - 每一步，黑王按照移动规则进行移动； - 黑王不能移动到有白棋子占据的格子上； - 黑王不能移动到被任何白棋子攻击的格子上。如果某个白棋子可以按照其移动规则一步到达某格，则该格被视为被攻击； - 白棋子不会移动。 请帮助黑王找到到达目标格子的最少步数，且不违反上述条件。黑王在任何时刻都不能离开棋盘。 黑王的移动规则如下。尽管白棋子不会移动，但它们能一步到达的格子都视为被攻击，黑王不能进入这些格子。 具体的棋子移动规则如下（除马以外，其他棋子不能越子）： - 王每次可以向水平、垂直或对角线方向移动一格。 - 车可以沿水平或垂直方向移动任意多个空格。 - 象可以沿对角线方向移动任意多个空格。 - 后可以沿水平、垂直或对角线方向移动任意多个空格。 - 马可以跳到最近的不在同一行、列或对角线的格子（可以理解为先水平移动两格再垂直移动一格，或先水平移动一格再垂直移动两格，即“L”型）。马不会被其他棋子阻挡，可以直接跳过。 棋盘上没有兵。 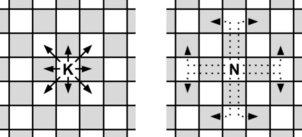 王和马的可能移动方式。虚线表示马可以越子。 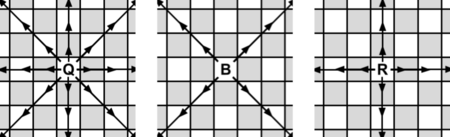 后、象、车的可能移动方式。

第一行包含两个整数 $x_s$ 和 $y_s$（$1 \le x_s \le 10^8$；$1 \le y_s \le 8$），表示黑王的起始坐标。 第二行包含两个整数 $x_t$ 和 $y_t$（$1 \le x_t \le 10^8$；$1 \le y_t \le 8$），表示黑王的目标格子的坐标。 第三行包含一个整数 $n$（$0 \le n \le 2000$），表示棋盘上的白棋子数量。 接下来 $n$ 行，每行包含一个字符 $t_i$ 和两个整数 $x_i$、$y_i$（$1 \le x_i \le 10^8$；$1 \le y_i \le 8$），表示第 $i$ 个白棋子的类型和坐标。棋子类型用如下大写英文字母表示： - K — 王 - Q — 后 - R — 车 - B — 象 - N — 马 棋盘上可以有任意数量、任意类型的白棋子，例如 $3$ 个白王或 $4$ 个白后。棋盘上没有兵。 输入的额外约束： - 没有格子被多个白棋子占据； - 黑王的起始格子和目标格子不同，且这两个格子都没有被白棋子占据，也没有被任何白棋子攻击。

输出一个整数，表示黑王到达目标格子的最小步数。如果无法到达，输出 $-1$。

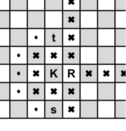
下图展示了第二个样例的解法。图中，K、R、s、t 分别表示白王、白车、起始格子和目标格子。粗体叉号标记了被白棋攻击的格子。粗体圆点表示黑王的最短路径。  由 ChatGPT 4.1 翻译