CF1770E Koxia and Tree

Imi 有一棵包含 $n$ 个结点的无向树，树的边编号为 $1$ 到 $n-1$。第 $i$ 条边连接结点 $u_i$ 和 $v_i$。树上有 $k$ 只蝴蝶。最初，第 $i$ 只蝴蝶位于结点 $a_i$。所有 $a$ 的取值两两不同。 Koxia 玩的游戏规则如下： - 对于 $i = 1, 2, \dots, n-1$，Koxia 以等概率将第 $i$ 条边定向为 $u_i \rightarrow v_i$ 或 $v_i \rightarrow u_i$。 - 对于 $i = 1, 2, \dots, n-1$，如果某只蝴蝶位于第 $i$ 条边的起点，且终点上没有蝴蝶，则这只蝴蝶会飞到终点。注意，这些操作是依次按 $1, 2, \dots, n-1$ 的顺序进行的，而不是同时进行。 - Koxia 从 $k$ 只蝴蝶中等概率选择两只，共有 $\frac{k(k-1)}{2}$ 种选择方式，然后她以这两只蝴蝶所在结点之间的距离 $^\dagger$ 作为得分。 现在，Koxia 想让你求出她得分的期望值，结果对 $998\,244\,353^\ddagger$ 取模。 $^\dagger$ 树上两个结点之间的距离是它们之间唯一一条简单路径上的边数。 $^\ddagger$ 形式化地说，设 $M = 998\,244\,353$。可以证明答案可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数且 $q \not\equiv 0 \pmod{M}$。输出等于 $p \cdot q^{-1} \bmod M$ 的整数。换句话说，输出一个整数 $x$，满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$。

第一行包含两个整数 $n$ 和 $k$（$2 \leq k \leq n \leq 3 \cdot 10^5$）——树的结点数和蝴蝶的数量。 第二行包含 $k$ 个整数 $a_1, a_2, \dots, a_k$（$1 \leq a_i \leq n$）——蝴蝶的初始位置。保证所有位置互不相同。 接下来 $n-1$ 行，第 $i$ 行包含两个整数 $u_i, v_i$（$1 \leq u_i, v_i \leq n$，$u_i \neq v_i$）——表示第 $i$ 条边连接的两个结点。 保证给定的边构成一棵树。

输出一个整数，表示 Koxia 得分的期望值，对 $998\,244\,353$ 取模。

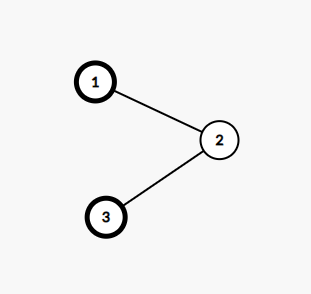
在第一个测试点中，树结构如下，含蝴蝶的结点用粗体表示。  只有 $2$ 只蝴蝶，因此选择蝴蝶的方式是唯一的。考虑以下 $4$ 种情况： - 边为 $1 \rightarrow 2$ 且 $2 \rightarrow 3$：蝴蝶从结点 $1$ 移动到结点 $2$，结点 $3$ 上的蝴蝶不动。此时结点 $2$ 和 $3$ 的距离为 $1$。 - 边为 $1 \rightarrow 2$ 且 $3 \rightarrow 2$：蝴蝶从结点 $1$ 移动到结点 $2$，但结点 $3$ 上的蝴蝶无法移动到 $2$，因为 $2$ 已被占据。此时结点 $2$ 和 $3$ 的距离为 $1$。 - 边为 $2 \rightarrow 1$ 且 $2 \rightarrow 3$：结点 $1$ 和 $3$ 上的蝴蝶都不动。此时结点 $1$ 和 $3$ 的距离为 $2$。 - 边为 $2 \rightarrow 1$ 且 $3 \rightarrow 2$：结点 $1$ 上的蝴蝶不动，结点 $3$ 上的蝴蝶移动到结点 $2$。此时结点 $1$ 和 $2$ 的距离为 $1$。 因此，Koxia 得分的期望值为 $\frac{1+1+2+1}{4} = \frac{5}{4}$，对 $998\,244\,353$ 取模后为 $748\,683\,266$。 在第二个测试点中，树结构如下，含蝴蝶的结点用粗体表示。Koxia 得分的期望值为 $\frac{11}{6}$，对 $998\,244\,353$ 取模后为 $831\,870\,296$。  由 ChatGPT 4.1 翻译