CF1770E Koxia and Tree

Imi has an undirected tree with $ n $ vertices where edges are numbered from $ 1 $ to $ n-1 $ . The $ i $ -th edge connects vertices $ u_i $ and $ v_i $ . There are also $ k $ butterflies on the tree. Initially, the $ i $ -th butterfly is on vertex $ a_i $ . All values of $ a $ are pairwise distinct. Koxia plays a game as follows: - For $ i = 1, 2, \dots, n - 1 $ , Koxia set the direction of the $ i $ -th edge as $ u_i \rightarrow v_i $ or $ v_i \rightarrow u_i $ with equal probability. - For $ i = 1, 2, \dots, n - 1 $ , if a butterfly is on the initial vertex of $ i $ -th edge and there is no butterfly on the terminal vertex, then this butterfly flies to the terminal vertex. Note that operations are sequentially in order of $ 1, 2, \dots, n - 1 $ instead of simultaneously. - Koxia chooses two butterflies from the $ k $ butterflies with equal probability from all possible $ \frac{k(k-1)}{2} $ ways to select two butterflies, then she takes the distance $ ^\dagger $ between the two chosen vertices as her score. Now, Koxia wants you to find the expected value of her score, modulo $ 998\,244\,353^\ddagger $ . $ ^\dagger $ The distance between two vertices on a tree is the number of edges on the (unique) simple path between them. $ ^\ddagger $ Formally, let $ M = 998\,244\,353 $ . It can be shown that the answer can be expressed as an irreducible fraction $ \frac{p}{q} $ , where $ p $ and $ q $ are integers and $ q \not \equiv 0 \pmod{M} $ . Output the integer equal to $ p \cdot q^{-1} \bmod M $ . In other words, output such an integer $ x $ that $ 0 \le x < M $ and $ x \cdot q \equiv p \pmod{M} $ .

The first line contains two integers $ n $ , $ k $ ( $ 2 \leq k \leq n \leq 3 \cdot {10}^5 $ ) — the size of the tree and the number of butterflies. The second line contains $ k $ integers $ a_1, a_2, \dots, a_k $ ( $ 1 \leq a_i \leq n $ ) — the initial position of butterflies. It's guaranteed that all positions are distinct. The $ i $ -th line in following $ n − 1 $ lines contains two integers $ u_i $ , $ v_i $ ( $ 1 \leq u_i, v_i \leq n $ , $ u_i \neq v_i $ ) — the vertices the $ i $ -th edge connects. It is guaranteed that the given edges form a tree.

Output a single integer — the expected value of Koxia's score, modulo $ 998\,244\,353 $ .

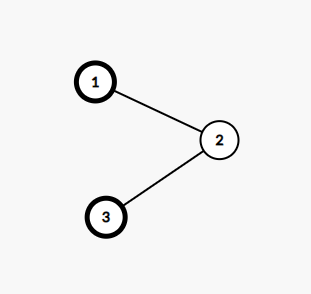In the first test case, the tree is shown below. Vertices containing butterflies are noted as bold. There are only $ 2 $ butterflies so the choice of butterflies is fixed. Let's consider the following $ 4 $ cases: - Edges are $ 1 \rightarrow 2 $ and $ 2 \rightarrow 3 $ : butterfly on vertex $ 1 $ moves to vertex $ 2 $ , but butterfly on vertex $ 3 $ doesn't move. The distance between vertices $ 2 $ and $ 3 $ is $ 1 $ . - Edges are $ 1 \rightarrow 2 $ and $ 3 \rightarrow 2 $ : butterfly on vertex $ 1 $ moves to vertex $ 2 $ , but butterfly on vertex $ 3 $ can't move to vertex $ 2 $ because it's occupied. The distance between vertices $ 2 $ and $ 3 $ is $ 1 $ . - Edges are $ 2 \rightarrow 1 $ and $ 2 \rightarrow 3 $ : butterflies on both vertex $ 1 $ and vertex $ 3 $ don't move. The distance between vertices $ 1 $ and $ 3 $ is $ 2 $ . - Edges are $ 2 \rightarrow 1 $ and $ 3 \rightarrow 2 $ : butterfly on vertex $ 1 $ doesn't move, but butterfly on vertex $ 3 $ move to vertex $ 2 $ . The distance between vertices $ 1 $ and $ 2 $ is $ 1 $ . Therefore, the expected value of Koxia's score is $ \frac {1+1+2+1} {4} = \frac {5} {4} $ , which is $ 748\,683\,266 $ after modulo $ 998\,244\,353 $ . In the second test case, the tree is shown below. Vertices containing butterflies are noted as bold. The expected value of Koxia's score is $ \frac {11} {6} $ , which is $ 831\,870\,296 $ after modulo $ 998\,244\,353 $ .