CF1770H Koxia, Mahiru and Winter Festival

Koxia 和 Mahiru 正在享受 Winter Festival。Winter Festival 的街道可以表示为一个 $n\times n$ 的无向网格图。正规地说，令顶点集合为 $\{ (i, j)∣1\le i, j\le n \}$，当且仅当两个顶点 $(i_1 , j_1 )$ 和 $(i_2 , j_2 )$ 满足条件 $\left\vert{i_1 - i_2}\right\vert+\left\vert{j_1 - j_2 }\right\vert=1$ 时，它们之间存在一条边连接。 如图一，是一张 $n = 3$ 的网个图(见原图)。Koxia 和 Mahiru 计划通过遍历 $2n$ 个路线参观冬季节日。尽管路线还没有计划好，但路线的终点已经确定如下： - 在第 $i$ 条路线中，他们希望从顶点 $(1, i)$ 出发，最终到达顶点 $(n, p_i)$，其中 $p$ 是长度为 $n$ 的排列。 - 在第 $(i+n)$ 条路线中，他们希望从顶点 $(i, 1)$ 出发，最终到达顶点 $(q_i, n)$，其中 $q$ 是长度为 $n$ 的排列。 一个大小为 $n = 3$ 的网络，要连接的点用相同的颜色表示，分别为 $p = [3, 2, 1]$ 和 $q = [3, 1, 2]$。你的任务是找到一个路径方案，即 $2n$ 条路径，每条路径连接指定的终点。我们将边的堵塞程度定义为路径方案中使用它的次数（包括双向）。为了确保 Koxia 和 Mahiru 不会因为穿越重复边而感到厌倦，请找到一种路径方案，使所有边中的最大堵塞程度最小化。 一个示例图(见原图)中解决方案——最大堵塞程度为 $2$，且在这种情况下是最优的。 样例 $2$ 和 $3$ 的输出如下所示：（见原图） 样例 $2$ 和 $3$ 的样例输出。最大堵塞程度分别为 $2$ 和 $1$。

第一行读入一个整数 $n$ $(2\le n\le 200)$，描述网格图大小。 第二行读入 $n$ 个整数 $p_1,p_2,...,p_n \ (1\le p_i\le n)$。 第三行读入 $n$ 个整数 $q_1,q_2,...,q_n \ (1\le q_i\le n)$。 保证 $p$ 和 $q$ 都是长度为 $n$ 的排列。

输出共 $2n$ 行，每一行描述一条路线。 前 $n$ 行应该描述从上到下的连接。第 $i$ 行应描述从起点 $(1，i)$ 开始，到终点 $(n，p_i)$ 结束的路线。 接下来的 $n$ 行应该描述从左到右的连接。第 $(i+n)$ 行应该描述从起点 $(i,1)$ 开始，到终点 $(qi,n)$ 结束的路线。 描述路线的每一行应以一个整数 $k(2 \le k \le 10^5)$ 开头，表示路线经过的顶点数，包括起点和终点。然后按顺序输出路线上的所有顶点。换句话说，如果路线是 $(x_1, y_1) \to (x_2, y_2) \to ... \to (x_k, y_k)$，则输出顺序为 $k \ x_1 \ y_1 \ x_2 \ y_2 ... x_k \ y_k$。注意对于 $1 \le i < k$ 应满足 $\left\vert{x_i - x_i+1}\right\vert + \left\vert{y_i - y_i+1}\right\vert = 1$。 如果最大拥堵程度最小的方案有多个，你输出任意一个即可。 ### **说明/提示**

The first example corresponds to the figures in the problem statement. The output for examples $ 2 $ and $ 3 $ respectively are visualized below: 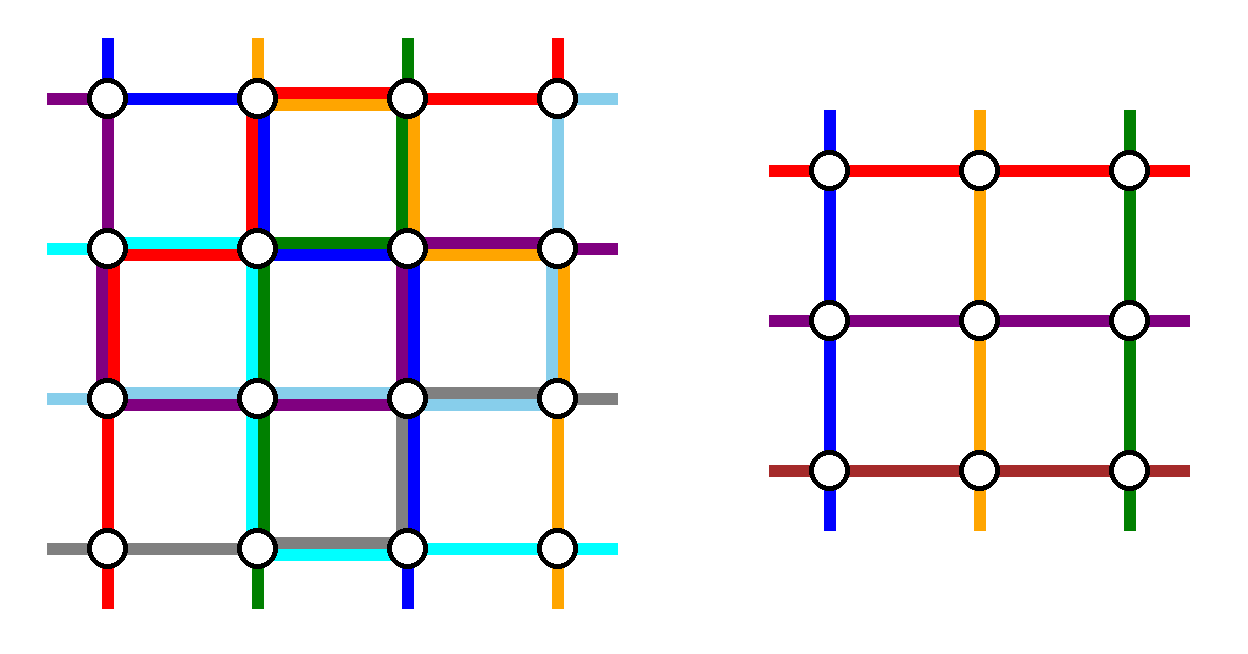 Sample output for examples $ 2 $ and $ 3 $ . Maximum congestions are $ 2 $ and $ 1 $ respectively.