CF1771D Hossam and (sub-)palindromic tree

Hossam has an unweighted tree $ G $ with letters in vertices. Hossam defines $ s(v, \, u) $ as a string that is obtained by writing down all the letters on the unique simple path from the vertex $ v $ to the vertex $ u $ in the tree $ G $ . A string $ a $ is a subsequence of a string $ s $ if $ a $ can be obtained from $ s $ by deletion of several (possibly, zero) letters. For example, "dores", "cf", and "for" are subsequences of "codeforces", while "decor" and "fork" are not. A palindrome is a string that reads the same from left to right and from right to left. For example, "abacaba" is a palindrome, but "abac" is not. Hossam defines a sub-palindrome of a string $ s $ as a subsequence of $ s $ , that is a palindrome. For example, "k", "abba" and "abhba" are sub-palindromes of the string "abhbka", but "abka" and "cat" are not. Hossam defines a maximal sub-palindrome of a string $ s $ as a sub-palindrome of $ s $ , which has the maximal length among all sub-palindromes of $ s $ . For example, "abhbka" has only one maximal sub-palindrome — "abhba". But it may also be that the string has several maximum sub-palindromes: the string "abcd" has $ 4 $ maximum sub-palindromes. Help Hossam find the length of the longest maximal sub-palindrome among all $ s(v, \, u) $ in the tree $ G $ . Note that the sub-palindrome is a subsequence, not a substring.

The first line contains one integer $ t $ ( $ 1 \le t \le 200 $ ) — the number of test cases. The first line of each test case has one integer number $ n $ ( $ 1 \le n \le 2 \cdot 10^3 $ ) — the number of vertices in the graph. The second line contains a string $ s $ of length $ n $ , the $ i $ -th symbol of which denotes the letter on the vertex $ i $ . It is guaranteed that all characters in this string are lowercase English letters. The next $ n - 1 $ lines describe the edges of the tree. Each edge is given by two integers $ v $ and $ u $ ( $ 1 \le v, \, u \le n $ , $ v \neq u $ ). These two numbers mean that there is an edge $ (v, \, u) $ in the tree. It is guaranteed that the given edges form a tree. It is guaranteed that sum of all $ n $ doesn't exceed $ 2 \cdot 10^3 $ .

For each test case output one integer — the length of the longest maximal sub-palindrome among all $ s(v, \, u) $ .

In the first example the maximal subpalindromes are "aaa" with letters in vertices $ 1, \, 3, \, 5 $ , or "aca" with letters in vertices $ 1, \, 4, \, 5 $ . 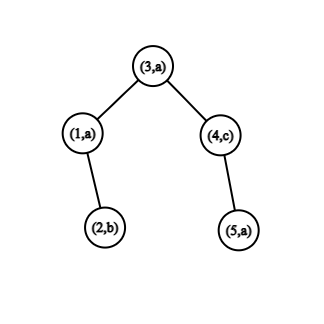 The tree from the first example.In the second example there is only one maximal palindrome "bacab" with letters in vertices $ 4, \, 2, \, 1, \, 5, \, 9 $ . 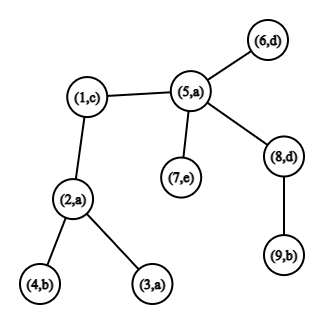 The tree from the second example.