CF1775D Friendly Spiders

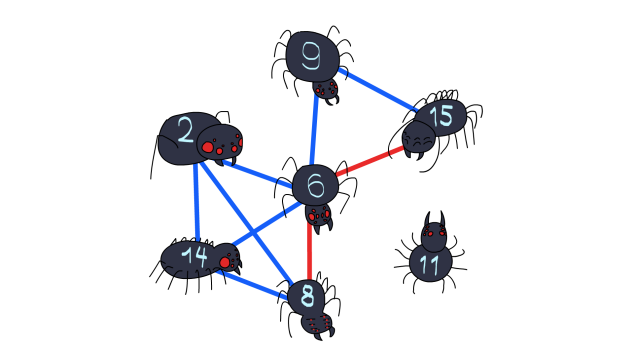
火星上有一种奇特的蜘蛛——二进制蜘蛛。 现在，火星科学家正在观察一个由 $n$ 只蜘蛛组成的群落，第 $i$ 只蜘蛛有 $a_i$ 条腿。 有些蜘蛛彼此是朋友。具体来说，如果第 $i$ 只和第 $j$ 只蜘蛛满足 $\gcd(a_i, a_j) \ne 1$，即存在某个整数 $k \ge 2$，使得 $a_i$ 和 $a_j$ 都能被 $k$ 整除，则这两只蜘蛛是朋友。这里 $\gcd(x, y)$ 表示整数 $x$ 和 $y$ 的最大公约数。 科学家们发现蜘蛛可以传递消息。如果两只蜘蛛是朋友，它们可以在一秒内直接传递消息。否则，蜘蛛必须把消息传递给它的朋友，再由朋友传递给朋友，依此类推，直到消息到达接收者。 让我们来看一个例子。 假设一只拥有八条腿的蜘蛛想要向一只拥有 $15$ 条腿的蜘蛛发送消息。它不能直接发送，因为 $\gcd(8, 15) = 1$。但它可以通过一只拥有六条腿的蜘蛛传递消息，因为 $\gcd(8, 6) = 2$ 且 $\gcd(6, 15) = 3$。因此，消息将在两秒内到达。 现在，科学家们正在观察第 $s$ 只蜘蛛想要向第 $t$ 只蜘蛛发送消息。研究人员假设蜘蛛总是以最优方式传递消息。因此，科学家们需要一个程序来计算发送消息所需的最短时间，并给出一条最优路径。 

输入的第一行包含一个整数 $n$（$2 \le n \le 3\cdot10^5$），表示蜘蛛群落中的蜘蛛数量。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 3\cdot10^5$），表示每只蜘蛛拥有的腿数。 第三行包含两个整数 $s$ 和 $t$（$1 \le s, t \le n$），表示需要传递消息的两只蜘蛛的编号。

如果无法在给定的两只蜘蛛之间传递消息，输出 $-1$。 否则，第一行输出整数 $t$（$t \ge 1$），表示参与消息传递的蜘蛛数量（即消息传递所需的最短时间加一）。第二行输出 $t$ 个不同的整数 $b_1, b_2, \ldots, b_t$（$1 \le b_i \le n$），表示消息传递路径上蜘蛛的编号，按发送者到接收者的顺序排列。 如果存在多条最优路径，输出任意一条即可。

第一个样例如上图所示。它展示了从第 $5$ 只蜘蛛（有八条腿）到第 $6$ 只蜘蛛（有 $15$ 条腿）最优的传递路径是经过第 $4$ 只蜘蛛（有六条腿）。 在第二个样例中，第 $7$ 只蜘蛛（有 $11$ 条腿）与任何蜘蛛都不是朋友，因此无法向它发送消息。 由 ChatGPT 4.1 翻译