CF1776I Spinach Pizza

Alberto 和 Beatrice 两兄妹必须一起吃菠菜披萨。但是他们都不喜欢吃菠菜，所以都想尽量少吃。 披萨的形状是一个由 $n$ 个位于平面的整数坐标的顶点 $(x_1, y_1), \, (x_2, y_2), \, \dots, \, (x_n, y_n)$ 组成的严格凸多边形。 兄妹俩决定以下面的方式吃掉披萨：从 Alberto 开始，兄妹轮流选择披萨剩余部分的一个顶点，吃掉由其两条相邻边决定的三角形（详情请查看样例解释）。在这样的前 $n - 3$ 轮，披萨上的顶点每轮会减少一个。在第 $(n - 2)$ 轮，披萨全部被吃掉，游戏结束。 假设 Alberto 和 Beatrice 以最优策略吃披萨，那么谁会吃掉**最多一半**披萨？你应该找出谁会赢，并帮他们适当地选择披萨片。请注意，如果 Alberto 和 Beatrice 都以最有策略吃披萨，那么他们最终吃掉的面积有可能正好是一半。

第一行包含一个整数 $n$ ( $4\le n \le 100$ ) 表示披萨的顶点数。 接下来的 $n$ 行分别包含两个整数 $x_i$ 和 $y_i$ ( $-10^6 \le x_i, y_i \le 10^6$ ) 代表披萨初始形状的多边形第 $i$ 个顶点的坐标。 保证该多边形是严格凸多边形，且其顶点按逆时针顺序给出。

首先，您应该打印一个字符串 $\texttt{Alberto}$ 或 $\texttt{Beatrice}$ 表示您将帮助获胜的兄弟姐妹。 然后，在接下来的 $n - 2$ 个回合中，你将与交互器交替选择一片披萨并取出它，如果你选择帮助 Alberto，则从你开始；如果你选择帮助 Beatrice，则从交互器开始。 - 当轮到你的时候，打印一行包含一个之前没有选择过的整数 $p$ ( $1 \leq p \leq n$ )，表示你想吃位于 $(x_p, y_p)$ 的顶点决定的那片披萨。 - 当轮到交互器时，读取一个整数 $q$ ( $1 \leq q \leq n$ )，表示交互器想吃由位于 $(x_q, y_q)$ 的顶点决定的披萨。 保证 $q$ 之前没有被选择过。 如果你的回答之一是错误的，交互器会立即终止，你的程序会收到判决 $\texttt{WRONG-ANSWER}$。否则，如果最后你的玩家吃掉了最多一半的披萨，你就会收到 $\texttt{CORRECT}$，否则就会收到 $\texttt{WRONG-ANSWER}$。 打印完一行后，不要忘记结束该行并刷新输出。要刷新输出，请使用： - 在 C 语言中使用： $\texttt{fflush(stdout)}$ ； - 在 C++ 中使用： $\texttt{fflush(stdout)}$ , $\texttt{cout

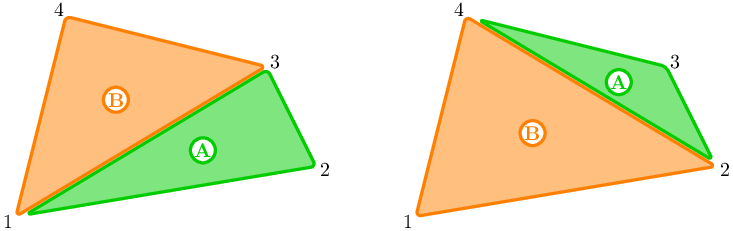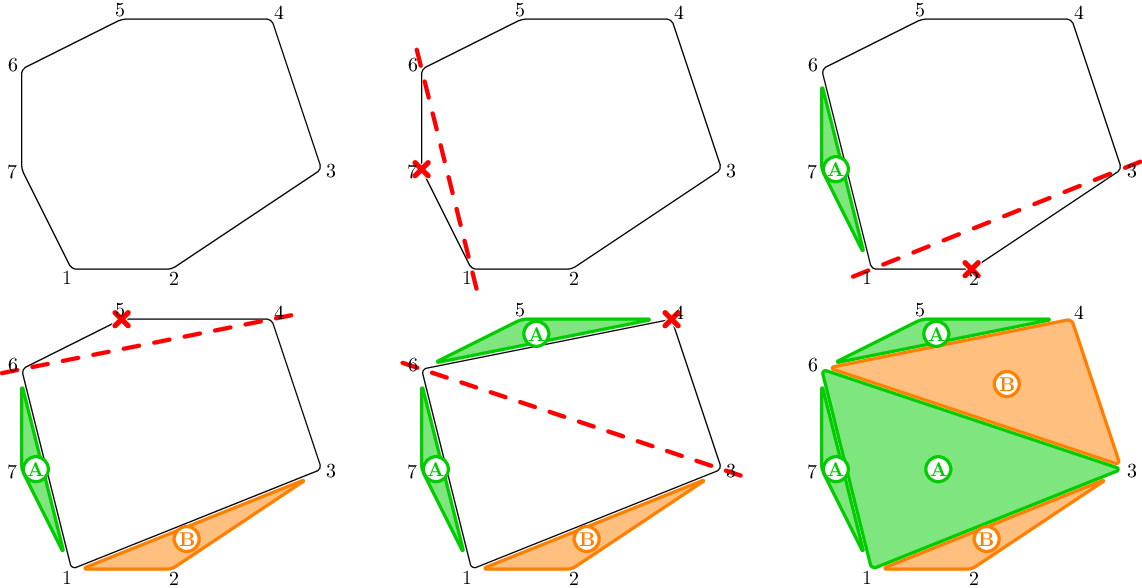
In the first sample, the pizza has area $ 15 $ . Alberto can eat less than half of the pizza by eating the slice around vertex $ 2 $ (which has area $ 6.5 $ ) or around vertex $ 3 $ (which has area $ 3.5 $ ). In the second sample, it can be proved that both players will eat exactly half of the pizza if they eat optimally. Therefore it is possible to choose to help either Alberto or Beatrice. In the third sample, it is possible to show that only Beatrice has a strategy to eat at most half of the pizza. The following is an example of a valid interaction (after reading the input): $ $$$ \begin{array}{|c|c|c|} \hline \textbf{Contestant} & \textbf{Judge} & \textbf{Explanation} \\ \hline \texttt{Beatrice} & & \text{The contestant will help Beatrice} \\ \hline & \texttt{7} & \text{Alberto eats the triangle with vertices $6$, $7$, $1$ and area $1$} \\ \hline \texttt{2} & & \text{Beatrice eats the triangle with vertices $1$, $2$, $3$ and area $2$} \\ \hline & \texttt{5} & \text{Alberto eats the triangle with vertices $4$, $5$, $6$ and area $1.5$} \\ \hline \texttt{4} & & \text{Beatrice eats the triangle with vertices $3$, $4$, $6$ and area $8$} \\ \hline & \texttt{6} & \text{Alberto eats the triangle with vertices $3$, $6$, $1$ and area $11$} \\ \hline \end{array} $ $ The total area eaten by Alberto is $ 13.5 $ and the total area eaten by Beatrice is $ 10$$$, which is less than half the area of the whole pizza. The actions performed by the contestant and the judge in this example of interaction may be non-optimal. The process is illustrated below: