CF1777D Score of a Tree

给定一棵有 $n$ 个节点的树，根节点为 $1$。每个节点在时刻 $t=0$ 时有一个值，取 $0$ 或 $1$。 在任意整数时刻 $t>0$，每个节点的值变为其所有子节点在时刻 $t-1$ 的值的按位异或（[bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR)）；叶子节点由于没有子节点，其值变为 $0$。 令 $S(t)$ 表示时刻 $t$ 所有节点的值之和。 令 $F(A)$ 表示对于初始赋值 $A$（即树上每个节点的 $0$ 或 $1$ 的初始状态），所有 $0 \le t \le 10^{100}$ 的 $S(t)$ 之和。 你的任务是计算所有 $2^n$ 种初始赋值 $A$ 的 $F(A)$ 之和，并对 $10^9+7$ 取模后输出。

每个测试点包含多组测试数据。第一行包含测试用例数 $t$（$1 \le t \le 10^5$）。 每组测试数据的第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$），表示树的节点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$，表示 $u$ 和 $v$ 之间有一条边（$1 \le u, v \le n$）。 保证所有测试用例的 $n$ 之和不超过 $2 \cdot 10^5$。

对于每组测试数据，输出答案对 $10^9+7$ 取模后的结果。

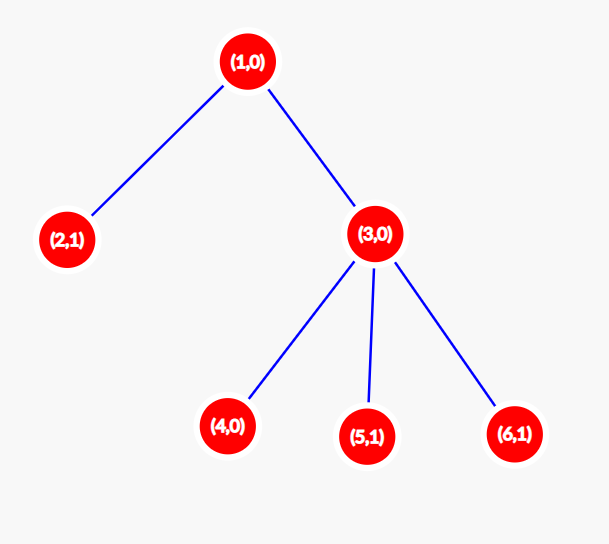
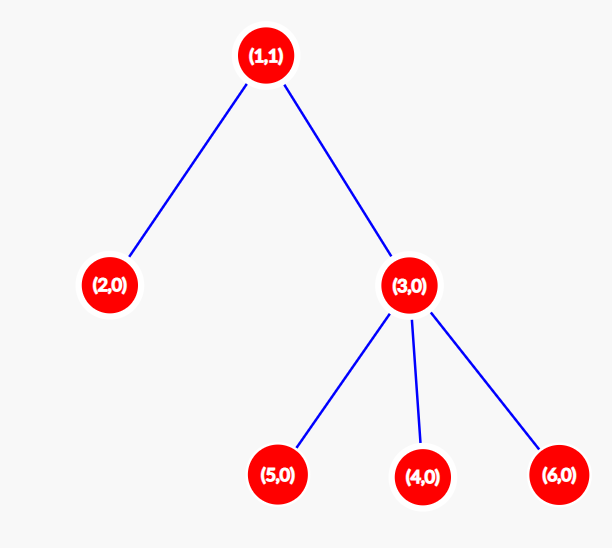
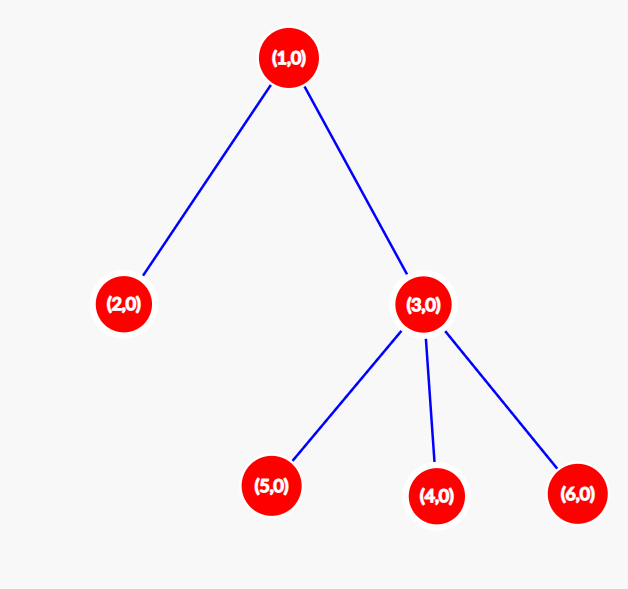
我们以初始配置 $A = [0,1,0,0,1,1]$（$A[i]$ 表示第 $i$ 个节点的值）为例，计算 $F(A)$。初始时（$t=0$），树如下图所示。每个节点中显示了节点编号和节点的值。此时 $S(0)=3$。  在 $t=1$ 时，配置变为 $[1,0,0,0,0,0]$。树如下图所示。$S(1)=1$。  在 $t=2$ 时，配置变为 $[0,0,0,0,0,0]$。树如下图所示。$S(2)=0$。  对于所有 $t>2$，树的状态不再变化，因此 $S(t)=0$。所以对于初始配置 $A=[0,1,0,0,1,1]$，有 $F(A)=3+1=4$。 对所有 $2^6$ 种初始配置进行上述过程，最终答案为 $\textbf{288}$。 由 ChatGPT 4.1 翻译