CF1777D Score of a Tree

You are given a tree of $ n $ nodes, rooted at $ 1 $ . Every node has a value of either $ 0 $ or $ 1 $ at time $ t=0 $ . At any integer time $ t>0 $ , the value of a node becomes the [bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) of the values of its children at time $ t - 1 $ ; the values of leaves become $ 0 $ since they don't have any children. Let $ S(t) $ denote the sum of values of all nodes at time $ t $ . Let $ F(A) $ denote the sum of $ S(t) $ across all values of $ t $ such that $ 0 \le t \le 10^{100} $ , where $ A $ is the initial assignment of $ 0 $ s and $ 1 $ s in the tree. The task is to find the sum of $ F(A) $ for all $ 2^n $ initial configurations of $ 0 $ s and $ 1 $ s in the tree. Print the sum modulo $ 10^9+7 $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). The description of the test cases follows. The first line of each test case contains $ n $ ( $ 1 \le n \le 2 \cdot 10^5 $ ) — the number of nodes in the tree. The next $ n-1 $ lines of each test case contain two integers each — $ u $ , $ v $ indicating an edge between $ u $ and $ v $ ( $ 1 \le u, v \le n $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

Output the sum modulo $ 10^9+7 $ for each test case.

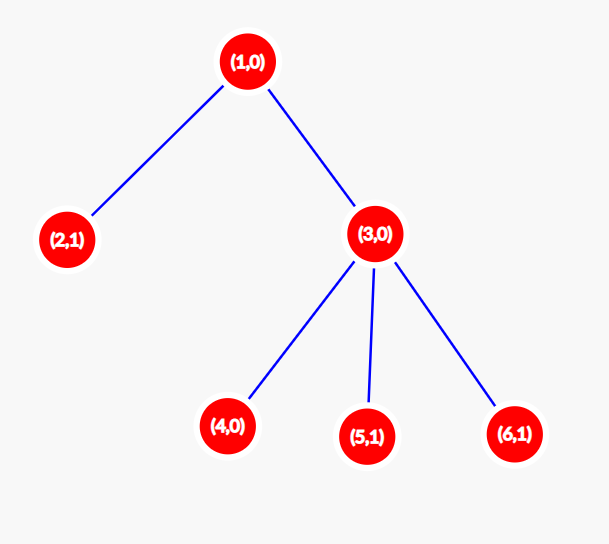Let us find $ F(A) $ for the configuration $ A = [0,1,0,0,1,1] $ ( $ A[i] $ denotes the value of node $ i $ ). Initially (at $ t = 0 $ ) our tree is as shown in the picture below. In each node, two values are shown: the number and the value of this node. $ S(0) $ for this configuration is $ 3 $ . At $ t = 1 $ the configuration changes to $ [1,0,0,0,0,0] $ . The tree looks as shown below. $ S(1) = 1 $ . 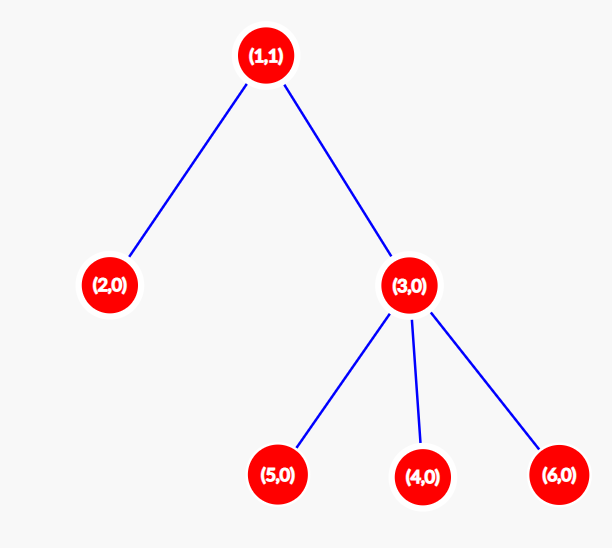At $ t = 2 $ the configuration changes to $ [0,0,0,0,0,0] $ . The tree looks as shown below. $ S(2) = 0 $ . 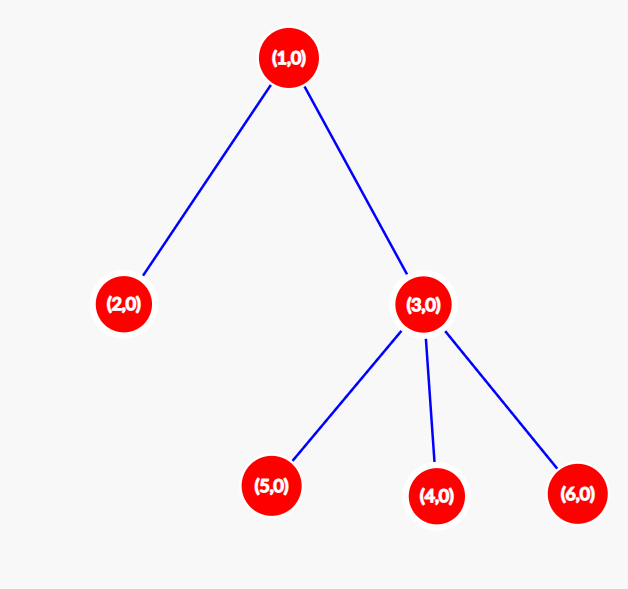For all $ t>2 $ , the graph remains unchanged, so $ S(t)=0 $ for all $ t > 2 $ . So, for the initial configuration $ A = [0,1,0,0,1,1] $ , the value of $ F(A) = 3 + 1 = 4 $ . Doing this process for all possible $ 2^{6} $ configurations yields us an answer of $ \textbf{288} $ .