CF1779F Xorcerer's Stones

Misha had been banned from playing chess for good since he was accused of cheating with an engine. Therefore, he retired and decided to become a xorcerer. One day, while taking a walk in a park, Misha came across a rooted tree with nodes numbered from $ 1 $ to $ n $ . The root of the tree is node $ 1 $ . For each $ 1\le i\le n $ , node $ i $ contains $ a_i $ stones in it. Misha has recently learned a new spell in his xorcery class and wants to test it out. A spell consists of: - Choose some node $ i $ ( $ 1 \leq i \leq n $ ). - Calculate the [bitwise XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) $ x $ of all $ a_j $ such that node $ j $ is in the subtree of $ i $ ( $ i $ belongs to its own subtree). - Set $ a_j $ equal to $ x $ for all nodes $ j $ in the subtree of $ i $ . Misha can perform at most $ 2n $ spells and he wants to remove all stones from the tree. More formally, he wants $ a_i=0 $ to hold for each $ 1\leq i \leq n $ . Can you help him perform the spells? A tree with $ n $ nodes is a connected acyclic graph which contains $ n-1 $ edges. The subtree of node $ i $ is the set of all nodes $ j $ such that $ i $ lies on the simple path from $ 1 $ (the root) to $ j $ . We consider $ i $ to be contained in its own subtree.

The first line contains a single integer $ n $ ( $ 2 \leq n \leq 2\cdot 10^5 $ ) — the size of the tree The second line contains an array of integers $ a_1,a_2,\ldots, a_n $ ( $ 0 \leq a_i \leq 31 $ ), describing the number of stones in each node initially. The third line contains an array of integers $ p_2,p_3,\ldots, p_n $ ( $ 1 \leq p_i \leq i-1 $ ), where $ p_i $ means that there is an edge connecting $ p_i $ and $ i $ .

If there is not a valid sequence of spells, output $ -1 $ . Otherwise, output a single integer $ q $ ( $ 0 \leq q \leq 2n $ ) in the first line — the number of performed spells. In the second line output a sequence of integers $ v_1,v_2,\ldots,v_q $ ( $ 1 \leq v_i \leq n $ ) — the $ i $ -th spell will be performed on the subtree of node $ v_i $ . Please note that order matters. If multiple solutions exist, output any. You don't have to minimize the number of operations.

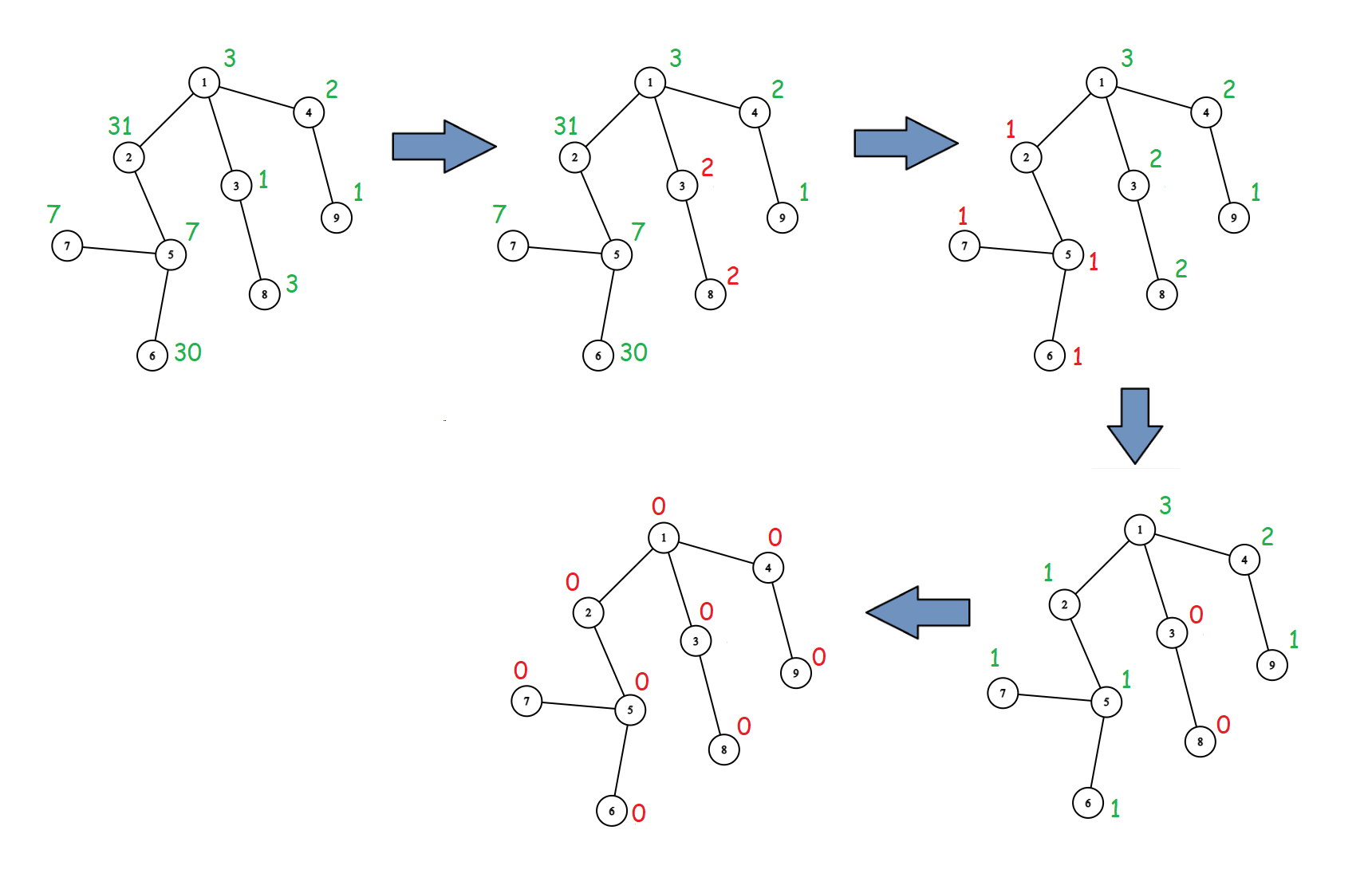
Please refer to the following pictures for an explanation of the third test. Only the first $ 4 $ spells are shown since the last $ 2 $ do nothing. The first picture represents the tree initially with the number of stones for each node written above it in green. Changes applied by the current spell are highlighted in red.