CF1779F Xorcerer's Stones
题目描述
米莎因为被指控使用引擎作弊,被永久禁止下棋。因此,他退休并决定成为一名“异或术士”。
一天,米莎在公园散步时,遇到了一棵有根树,节点编号为 $1$ 到 $n$。树的根节点是节点 $1$。
对于每个 $1\le i\le n$,节点 $i$ 中有 $a_i$ 颗石头。米莎最近在异或术课上学到了一种新咒语,想要试一试。每次施法包括:
- 选择某个节点 $i$($1 \leq i \leq n$)。
- 计算所有属于 $i$ 的子树的节点 $j$ 的 $a_j$ 的按位异或和 $x$($i$ 自己也属于自己的子树)。
- 将所有属于 $i$ 的子树的节点 $j$ 的 $a_j$ 都赋值为 $x$。
米莎最多可以施展 $2n$ 次咒语,他想要把树上的所有石头都移除。更正式地说,他希望对于每个 $1\leq i \leq n$ 都有 $a_i=0$。你能帮他完成这个目标吗?
一棵有 $n$ 个节点的树是一个连通无环图,包含 $n-1$ 条边。节点 $i$ 的子树是所有满足从根节点 $1$ 到 $j$ 的简单路径上经过 $i$ 的节点 $j$ 的集合。我们认为 $i$ 也包含在自己的子树中。
输入格式
第一行包含一个整数 $n$($2 \leq n \leq 2\cdot 10^5$),表示树的大小。
第二行包含一个整数数组 $a_1,a_2,\ldots, a_n$($0 \leq a_i \leq 31$),表示每个节点初始时的石头数。
第三行包含一个整数数组 $p_2,p_3,\ldots, p_n$($1 \leq p_i \leq i-1$),其中 $p_i$ 表示存在一条连接 $p_i$ 和 $i$ 的边。
输出格式
如果不存在合法的施法序列,输出 $-1$。
否则,第一行输出一个整数 $q$($0 \leq q \leq 2n$),表示施法的次数。
第二行输出一个长度为 $q$ 的整数序列 $v_1,v_2,\ldots,v_q$($1 \leq v_i \leq n$),表示第 $i$ 次施法作用于节点 $v_i$ 的子树。请注意,顺序是有影响的。
如果有多种方案,输出任意一种即可。你不需要最小化操作次数。
说明/提示
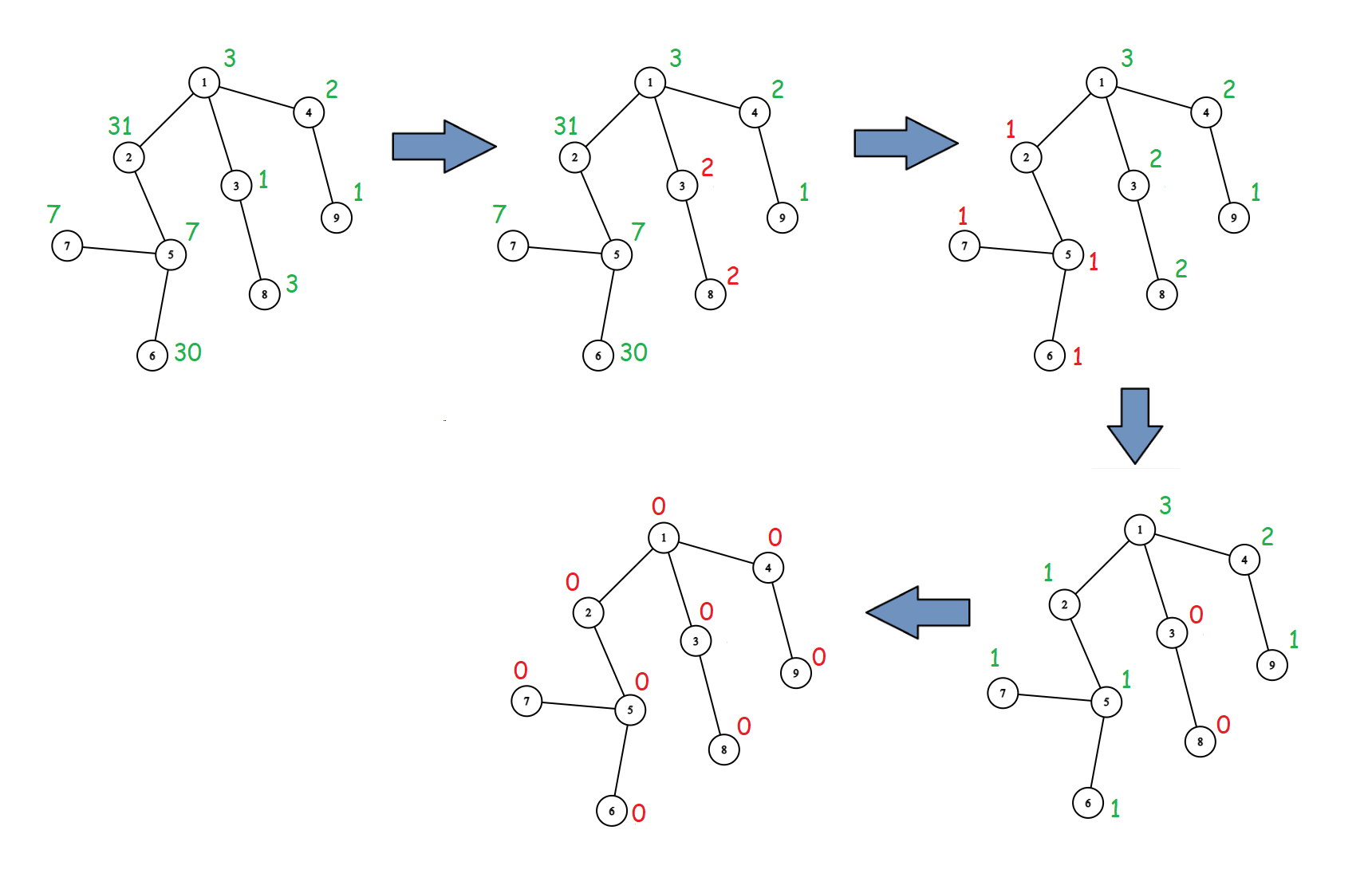
请参考下图理解第三个测试点的解释。只展示了前 $4$ 次施法,因为最后 $2$ 次没有效果。第一张图表示初始树,每个节点上方绿色数字为石头数。当前施法导致的变化用红色高亮。
由 ChatGPT 4.1 翻译