CF1779G The Game of the Century

有一个村庄呈正三角形，外围被三条长度为 $n$ 的路径包围，内部被 $3n-3$ 条另外的路径分割成 $n^2$ 个更小的正三角形（$n=3$ 时如图）。每条路径由一些方向一致的有向边组成，顺次连接相邻的路口。 可以翻转任意条有向边的方向，求把让图中每个点都可以到达其他所有点的最小翻转次数。

第一行一个整数 $t(1\le t\le10^4)$，表示数据组数。 每组数据第一行一个正整数 $n(1\le n\le 10^5)$，表示村庄大小。 接下来三行每行一个长度为 $n$ 的 $01$ 串 $s_i$。$s_{i,j}$ 描述与 $i$ 表示的路径平行的路径 $j$ 的方向（$i$ 的位置与方向见上图），顺序按长度从小到大排列。 若 $s_{i,j}$ 为 $1$，表示第 $j$ 层与 $i$ 表示的路径方向相同。反之，表示第 $j$ 层与 $i$ 表示的路径方向不同。 保证 $\sum n\le10^5$。

共 $t$ 行，每行一个整数，表示最小翻转次数。

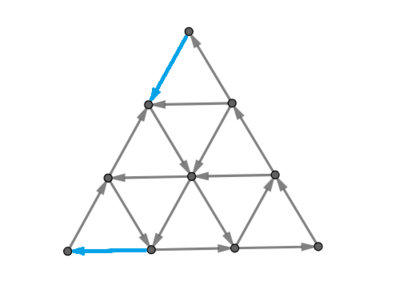The first example corresponds to the picture in the statement. There exist multiple solutions that invert the traffic direction of exactly $ 2 $ road segments, but inverting only $ 1 $ road segment never makes it possible to reach every intersection from any other. One of the possible solutions is shown in the picture below in which the inverted road segments are highlighted in blue. In the second example, the answer is $ 0 $ since it is already possible to reach every intersection from any other.