CF1780E Josuke and Complete Graph

Josuke 收到了一个巨大的无向带权完全图 $G$ 作为他祖父的礼物。该图形包含$10^{18}$ 个顶点。 这个礼物的特点是不同顶点 $u$ 和 $v$ 之间的边的权重等于 $\gcd(u,v)$ 。 Josuke 决定制作一个新的图 $G'$。为此，他选择两个整数 $l\le r$ ，并删除除 $l\le v\le r$ 的顶点 $v$ 之外的所有顶点以及与其相连的边。 现在 Josuke 想知道 $G'$ 中有的边多少种不同的权重。

第 $1$ 行一个整数 $t\;(1\le t\le100)$ ，表示数据组数。 接下来 $t$ 行每行两个整数 $l,r\;(1\le l\le r\le10^{18},l\le10^9\;)$ ，表示一组数据中的 $l,r$ 。

每行一个整数，表示每组数据 $G'$ 中不同权重的边的数量。 Translated by @[w9095](https://www.luogu.com.cn/user/569235)

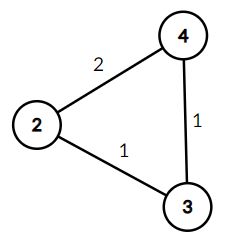 The graph $ G' $ for the first test case.The picture above shows that the graph has $ 2 $ different weights. In the fifth test case, there is only one vertex from which no edges originate, so the answer is $ 0 $ .