CF1780E Josuke and Complete Graph

Josuke received a huge undirected weighted complete $ ^\dagger $ graph $ G $ as a gift from his grandfather. The graph contains $ 10^{18} $ vertices. The peculiarity of the gift is that the weight of the edge between the different vertices $ u $ and $ v $ is equal to $ \gcd(u, v)^\ddagger $ . Josuke decided to experiment and make a new graph $ G' $ . To do this, he chooses two integers $ l \le r $ and deletes all vertices except such vertices $ v $ that $ l \le v \le r $ , and also deletes all the edges except between the remaining vertices. Now Josuke is wondering how many different weights are there in $ G' $ . Since their count turned out to be huge, he asks for your help. $ ^\dagger $ A complete graph is a simple undirected graph in which every pair of distinct vertices is adjacent. $ ^\ddagger $ $ \gcd(x, y) $ denotes the [greatest common divisor (GCD)](https://en.wikipedia.org/wiki/Greatest_common_divisor) of the numbers $ x $ and $ y $ .

The first line contains one integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases. The first line of each test case contains two numbers $ l $ , $ r $ ( $ 1 \le l \le r \le 10^{18} $ , $ l \le 10^9 $ ).

For each test case print a single number — the number of different weights among the remaining edges.

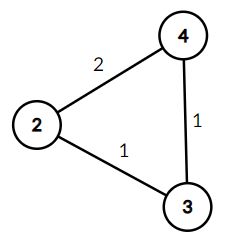 The graph $ G' $ for the first test case.The picture above shows that the graph has $ 2 $ different weights. In the fifth test case, there is only one vertex from which no edges originate, so the answer is $ 0 $ .