CF1783G Weighed Tree Radius

给你一个$n$个点的树和$n-1$条边。第$i$个点的初始权值为$a_i$。 定义结点$v$到结点$u$的距离$d_v(u)$等于$v$和$u$之间的边的数量。注意:$d_v(u)=d_u(v),d_v(v)=0$ 定义结点$v$到结点$u$的权值距离$w_v(u)=d_v(u)+a_u$。注意：$w_v(v)=a_v,w_v(u) \neq w_u(v)$如果$a_u \neq a_v$ 与通常的距离类似，让我们定义结点$v$的偏心距$e(v)$是从$v$到其他结点的最大**权值距离（包括$v$本身）**，即$e(v)=\max\limits_{1\leq u \leq n} w_v(u)$。 最后，我们定义树的半径$r$是所有偏心距的最小值，即$r=\min\limits_{1\leq v\leq n} e(v)$ 你需要对$m$次询问进行回答，对于第$j$次询问，给出两个数$v_j$和$x_j$，表示将$a_{v_j}$的值修改为$x_j$。 在每次询问后，输出当前该树的半径$r$。

第一行包含一个整数$n(2\leq n \leq2\cdot10^5)$，表示树的结点个数。 第二行包含$n$个整数$a_1,\dots,a_n(0\leq a_i\leq 10^6)$，表示每个节点的初始权值。 接下来$n-1$行表示树的边。第$i$行包含两个整数$u_i$和$v_i(1\leq u_i,v_i\leq n;u_i \neq v_i)$，表示树的一条边。 接下来一行包含一个整数$m$，表示查询的个数。 接下来$m$行每行包含一个询问。第$j$个询问包含两个整数$v_j$和$x_j(1\leq v_j\leq n;0\leq x_j\leq10^6)$，表示询问的结点和该结点的新权值。

输出$m$个整数，表示每个查询后树的半径$r$。

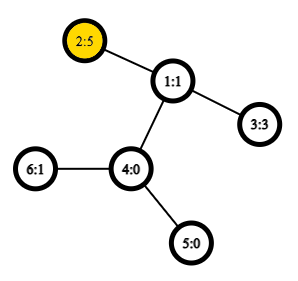
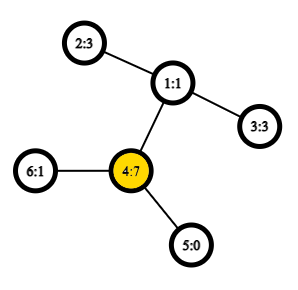
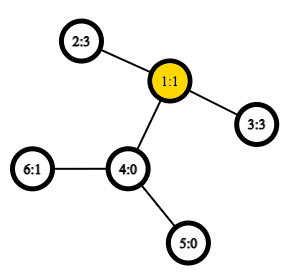
第一个询问后，你会得到下面这样的树：  图中被标记的结点是偏心距$e(v)$最小的结点，即$r=e(4)=7$。其他结点的偏心距如下:$e(1)=8,e(2)=9,e(3)=9,e(5)=8,e(6)=8$。 第二个询问后，你会得到下面这样的树：  半径$r=e(1)=4$ 第三个询问后，半径$r=e(2)=5$。