CF1783G Weighed Tree Radius

You are given a tree of $ n $ vertices and $ n - 1 $ edges. The $ i $ -th vertex has an initial weight $ a_i $ . Let the distance $ d_v(u) $ from vertex $ v $ to vertex $ u $ be the number of edges on the path from $ v $ to $ u $ . Note that $ d_v(u) = d_u(v) $ and $ d_v(v) = 0 $ . Let the weighted distance $ w_v(u) $ from $ v $ to $ u $ be $ w_v(u) = d_v(u) + a_u $ . Note that $ w_v(v) = a_v $ and $ w_v(u) \neq w_u(v) $ if $ a_u \neq a_v $ . Analogically to usual distance, let's define the eccentricity $ e(v) $ of vertex $ v $ as the greatest weighted distance from $ v $ to any other vertex (including $ v $ itself), or $ e(v) = \max\limits_{1 \le u \le n}{w_v(u)} $ . Finally, let's define the radius $ r $ of the tree as the minimum eccentricity of any vertex, or $ r = \min\limits_{1 \le v \le n}{e(v)} $ . You need to perform $ m $ queries of the following form: - $ v_j $ $ x_j $ — assign $ a_{v_j} = x_j $ . After performing each query, print the radius $ r $ of the current tree.

The first line contains the single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^5 $ ) — the number of vertices in the tree. The second line contains $ n $ integers $ a_1, \dots, a_n $ ( $ 0 \le a_i \le 10^6 $ ) — the initial weights of vertices. Next $ n - 1 $ lines contain edges of tree. The $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \neq v_i $ ) — the corresponding edge. The given edges form a tree. The next line contains the single integer $ m $ ( $ 1 \le m \le 10^5 $ ) — the number of queries. Next $ m $ lines contain queries — one query per line. The $ j $ -th query contains two integers $ v_j $ and $ x_j $ ( $ 1 \le v_j \le n $ ; $ 0 \le x_j \le 10^6 $ ) — a vertex and it's new weight.

Print $ m $ integers — the radius $ r $ of the tree after performing each query.

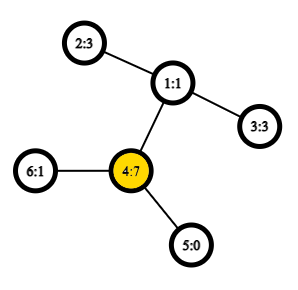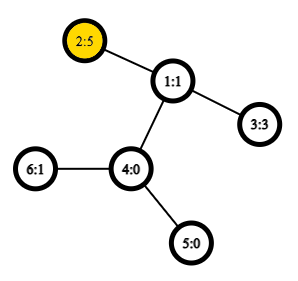
After the first query, you have the following tree:  The marked vertex in the picture is the vertex with minimum $ e(v) $ , or $ r = e(4) = 7 $ . The eccentricities of the other vertices are the following: $ e(1) = 8 $ , $ e(2) = 9 $ , $ e(3) = 9 $ , $ e(5) = 8 $ , $ e(6) = 8 $ .The tree after the second query:  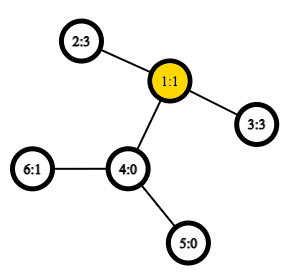The radius $ r = e(1) = 4 $ .After the third query, the radius $ r = e(2) = 5 $ :