CF178B2 Greedy Merchants

In ABBYY a wonderful Smart Beaver lives. This time, he began to study history. When he read about the Roman Empire, he became interested in the life of merchants. The Roman Empire consisted of $ n $ cities numbered from $ 1 $ to $ n $ . It also had $ m $ bidirectional roads numbered from $ 1 $ to $ m $ . Each road connected two different cities. Any two cities were connected by no more than one road. We say that there is a path between cities $ c_{1} $ and $ c_{2} $ if there exists a finite sequence of cities $ t_{1},t_{2},...,t_{p} $ $ (p>=1) $ such that: - $ t_{1}=c_{1} $ - $ t_{p}=c_{2} $ - for any $ i $ $ (1

The first input line contains two integers $ n $ and $ m $ , separated by a space, $ n $ is the number of cities, and $ m $ is the number of roads in the empire. The following $ m $ lines contain pairs of integers $ a_{i} $ , $ b_{i} $ $ (1

Print exactly $ k $ lines, the $ i $ -th line should contain a single integer $ d_{i} $ — the number of dinars that the $ i $ -th merchant paid.

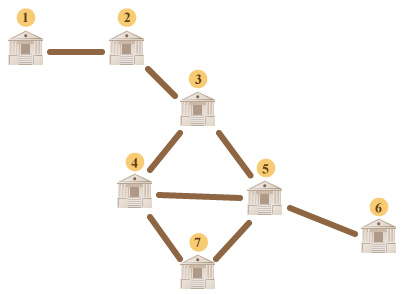The given sample is illustrated in the figure below. Let's describe the result for the first merchant. The merchant's warehouse is located in city $ 1 $ and his shop is in city $ 5 $ . Let us note that if either road, $ (1,2) $ or $ (2,3) $ is destroyed, there won't be any path between cities $ 1 $ and $ 5 $ anymore. If any other road is destroyed, the path will be preserved. That's why for the given merchant the answer is $ 2 $ .