CF178B2 Greedy Merchants

在 ABBYY 中住着一只聪明的海狸。这一次，它开始研究历史。当它读到有关罗马帝国的内容时，它对商人的生活产生了兴趣。 罗马帝国由编号从 $1$ 到 $n$ 的 $n$ 个城市组成。它还拥有 $m$ 条双向道路，编号从 $1$ 到 $m$。每条路连接两个不同的城市，任何两个城市之间最多只有一条路相连。 如果存在一个有限的城市序列 $t_1, t_2, \ldots, t_p$（$p \geq 1$），使得： - $t_1 = c_1$ - $t_p = c_2$ - 对于任意 $i$（$1 \leq i < p$），城市 $t_i$ 和 $t_{i+1}$ 都通过一条道路相连。 则称城市 $c_1$ 和 $c_2$ 之间存在一条路径。 我们知道罗马帝国的任何两个城市之间都存在一条路径。 在帝国中有 $k$ 个商人，编号从1到k。对于每个商人，可以用 $s_i$ 和 $l_i$ 表示，其中 $s_i$ 是这个商人仓库所在城市的编号，$l_i$ 是他的商店所在的城市编号。商店和仓库可能位于不同的城市，因此商人们需要将货物从仓库运送到商店。 如果某一条路的破坏会让一个商人的城市和仓库之间不再存在“路径”，那么称这条路对于该商人是“重要的道路”。罗马帝国的商人们非常贪婪，因此每个商人只为对他“重要的道路”缴纳税款（$1$ 元）。换句话说，每个商人支付 $d_i$ 元的税款，其中 $d_i$（$d_i \geq 0$）是对该商人“重要的道路”的数量。 收税日到来，聪明的海狸想要计算每个商人需要缴纳的税，他需要你的帮助。

第一行包含两个整数 $n$ 和 $m$，用空格隔开，$n$ 是城市的数量，$m$ 是帝国中道路的数量。 接下来的 $m$ 行每行两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$, $a_i \neq b_i$），用空格隔开，表示帝国中第 $i$ 条道路的起始城市和终止城市。数据保证任何两个城市之间最多只有一条道路相连，并且任何两个城市之间都存在路径。 下一行一个单独的整数 $k$，表示商人的数量。 接下来的 $k$ 行每行两个整数 $s_i$ 和 $l_i$（$1 \leq s_i, l_i \leq n$），用空格隔开。$s_i$ 是第 $i$ 个商人仓库所在城市的编号，而 $l_i$ 是第 $i$ 个商人商店所在城市的编号。

输出 $k$ 行，第 $i$ 行应包含一个单独的整数 $d_i$，表示第 $i$ 个商人要交多少元税。

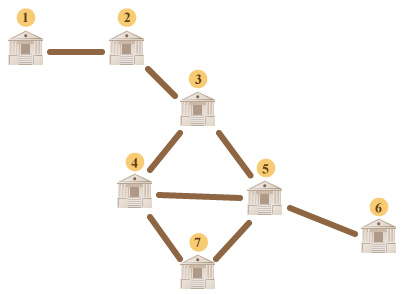The given sample is illustrated in the figure below. Let's describe the result for the first merchant. The merchant's warehouse is located in city $ 1 $ and his shop is in city $ 5 $ . Let us note that if either road, $ (1,2) $ or $ (2,3) $ is destroyed, there won't be any path between cities $ 1 $ and $ 5 $ anymore. If any other road is destroyed, the path will be preserved. That's why for the given merchant the answer is $ 2 $ .