CF178D3 Magic Squares

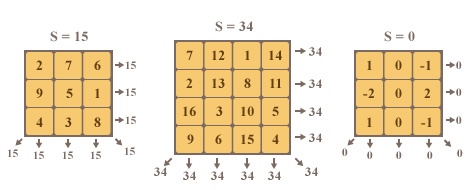
ABBYY 的聪明海狸喜欢谜题。他最喜爱的谜题之一是幻方。最近他想出了一个自动化解决这个谜题的方法，并决定将这个挑战作为 ABBYY Cup 的赛题。 幻方是一个大小为 $n \times n$ 的矩阵，其元素均为整数。该矩阵每行的数字之和等于某个数 $s$，每列的数字之和也等于 $s$。此外，主对角线上元素之和等于 $s$，副对角线上元素之和同样等于 $s$。下图展示了幻方的示例：  现给定包含 $n^{2}$ 个整数 $a_{i}$ 的集合，要求将这些数字填入一个 $n \times n$ 的方阵，使其构成幻方。注意每个数字在矩阵中出现的次数必须与其在原集合中出现的次数完全相同。 **题目保证解存在！**

第一行输入包含一个整数 $n$。 第二行包含 $n^{2}$ 个整数 $a_{i}$（$ -10^{8} \leq a_{i} \leq 10^{8} $），以空格分隔。 各分数段对应的输入限制如下： - **20 分** 的输入限制： - $1 \leq n \leq 3$ - **50 分** 的输入限制： - $1 \leq n \leq 4$ - 保证 $a_{i}$ 中不同数字的数量不超过 9 个 - **100 分** 的输入限制： - $1 \leq n \leq 4$

第一行输出一个整数 $s$。 接下来 $n$ 行每行输出 $n$ 个整数，用空格分隔，描述构造的幻方。构造的幻方需满足行、列及两条对角线的和均为 $s$。若存在多个解，可输出任意一个合法解。 翻译由 DeepSeek R1 完成