CF1790F Timofey and Black-White Tree

Timofey 来到著名的夏令营，发现了一棵有 $n$ 个点的树。树是一种无环连通无向图。 这棵树上，除了 $c_0$ 以外的所有点都是白色的。点 $c_0$ 是黑色的。 Timofey 想要把这棵树上的所有点都染成黑色。为此，他会进行 $n-1$ 次操作。在第 $i$ 次操作中，他选择当前为白色的点 $c_i$，并将其染成黑色。 我们定义树的“positivity”为所有不同黑色点对之间的最小距离。点 $v$ 和 $u$ 之间的距离是从 $v$ 到 $u$ 的路径上的边数。 每次操作后，Timofey 都想知道当前树的 positivity。

第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n, c_0$（$2 \le n \le 2 \cdot 10^5$，$1 \le c_0 \le n$），分别表示树的节点数和初始黑色节点的编号。 每个测试用例的第二行包含 $n-1$ 个互不相同的整数 $c_1, c_2, \dots, c_{n-1}$（$1 \le c_i \le n$，$c_i \ne c_0$），其中 $c_i$ 表示第 $i$ 次操作中被染成黑色的节点编号。 接下来的 $n-1$ 行，每行包含两个整数 $v_i, u_i$（$1 \le v_i, u_i \le n$），表示树中的一条边。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出 $n-1$ 个整数，每个整数占一行。 第 $i$ 个整数表示前 $i$ 次操作后树的 positivity。

在第一个测试用例中，第二次操作后，树的结构如下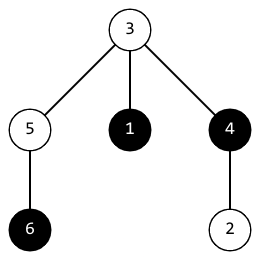： 点 $1$ 和 $6$ 之间的距离是 $3$，点 $4$ 和 $6$ 之间的距离是 $3$，点 $1$ 和 $4$ 之间的距离是 $2$。此时树的 positivity 等于这些距离的最小值，即 $2$。 在第三个测试用例中，第四次操作后，树的结构如下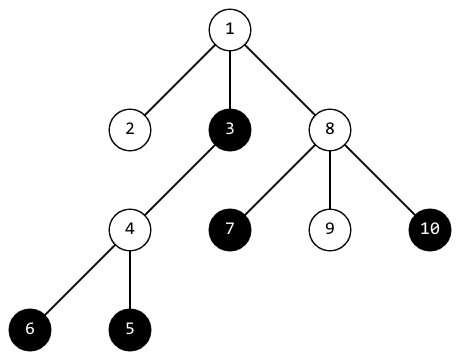： 此时树的 positivity 为 $2$。 由 ChatGPT 4.1 翻译