CF1790G Tokens on Graph
题目描述
给定一个无向连通图,其中一些顶点上有棋子和/或奖励。现在有一个关于你自己的游戏。
你可以按照以下规则移动棋子:
- 游戏开始时,你可以进行恰好一次操作:将任意一个棋子移动到任意相邻的顶点。
- 如果棋子的移动以奖励点结束,则你可以用任意其他棋子再进行一次操作。
你可以以任意顺序使用不同的奖励。同一个奖励可以被无限次使用。奖励在游戏过程中不会移动。
同一顶点可以同时有多个棋子,但初始时每个顶点最多只有一个棋子。
编号为 $1$ 的顶点是终点,你的任务是判断是否可以通过上述规则,将任意一个棋子移动到终点。如果有棋子一开始就在 $1$ 号顶点,则视为已经获胜。
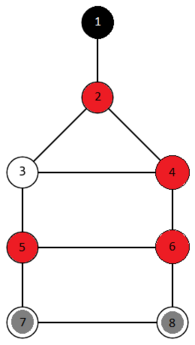 终点为黑色,奖励为红色,棋子为灰色。例如,对于给定的图,你可以通过如下操作序列,将第 $8$ 号顶点的棋子移动到终点:
1. 从第 $8$ 号顶点移动到第 $6$ 号顶点。
2. 从第 $7$ 号顶点移动到第 $5$ 号顶点。
3. 从第 $6$ 号顶点移动到第 $4$ 号顶点。
4. 从第 $5$ 号顶点移动到第 $6$ 号顶点。
5. 从第 $4$ 号顶点移动到第 $2$ 号顶点。
6. 从第 $6$ 号顶点移动到第 $4$ 号顶点。
7. 从第 $2$ 号顶点移动到第 $1$ 号顶点,即终点。
输入格式
输入的第一行包含一个整数 $t$($1 \le t \le 10^4$),表示测试用例的数量。接下来是每个测试用例的描述。
每个测试用例的第一行包含两个整数 $n$ 和 $m$($1 \le n \le 2 \cdot 10^5$,$0 \le m \le 2 \cdot 10^5$),分别表示图的顶点数和边数。
每个测试用例的第二行包含两个整数 $p$ 和 $b$($1 \le p \le n, 0 \le b \le n$),分别表示棋子的数量和奖励的数量。
每个测试用例的第三行包含 $p$ 个不同的整数,范围为 $1$ 到 $n$,表示棋子所在的顶点编号。
每个测试用例的第四行包含 $b$ 个不同的整数,范围为 $1$ 到 $n$,表示奖励所在的顶点编号。注意 $b$ 可能为 $0$,此时该行为空。
同一顶点可以同时有棋子和奖励。
接下来 $m$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \le u_i, v_i \le n$,$u_i \ne v_i$),表示第 $i$ 条边连接的两个顶点。任意一对顶点之间最多只有一条边。保证给定的图是连通的,即从任意顶点都可以通过边到达任意其他顶点。
不同测试用例之间用一个空行隔开。
保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$,所有测试用例中 $m$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每个测试用例,输出一行 YES,如果可以用某个棋子到达终点,否则输出 NO。
YES 和 NO 不区分大小写(例如 yEs、yes、Yes 和 YES 都视为正答)。
说明/提示
- 第一个测试用例的解释见题面。
- 第二个测试用例中,只有一个棋子且只能移动一次,无法到达终点。
- 第三个测试用例中,棋子可以在 $1$ 步内到达终点。
- 第四个测试用例中,只需从 $2$ 号顶点移动到 $1$ 号顶点即可。
- 第六个测试用例中,棋子一开始就在 $1$ 号顶点,因此直接获胜。
由 ChatGPT 4.1 翻译