CF1794E Labeling the Tree with Distances

现在给你一棵有 $n$ 个结点的树，结点编号为 $1$ 到 $n$；以及一个含有 $n - 1$ 个数的整数数列 $a_1, a_2, \ldots, a_{n - 1}$。一棵树是一个无向无环连通图。你可以使用列表中的每个元素来标记一个点，但任何顶点都不能被标记两次。你可以用任意整数来标注剩下的那唯一一个没有标记的点。 当且仅当存在一种标记方案使得对于每个节点 $i$ 的标记都等于 $i$ 到 $x$ 的距离时，我们称一个结点 $x$ 是一个『好点』。在树上，点 $s$ 到点 $t$ 的距离是从 $s$ 到 $t$ 的所有路径中边的数量的最小值。 请找出所有『好点』。

输入共有 $n + 1$ 行。 第一行仅有一个整数 $n$（$ 2 \le n \le 2 \times 10^5 $），表示树上点的个数。 第二行有 $n - 1$ 个整数，表示数列 $ a_1,a_2,\ldots,a_{n-1} $。保证该数列的任意数 $a_i$ 均满足 $ 0 \le a_i < n $。 最后 $n - 1$ 行，每行有两个整数 $u$ 和 $v$（$ 1\le u,v\le n $），表明结点 $u$ 和结点 $v$ 有一条无向边。数据保证输入的图是一棵树。

输出共 $2$ 行。 第一行，输出『好点』的数量。第二行，按升序排列输出所有『好点』。

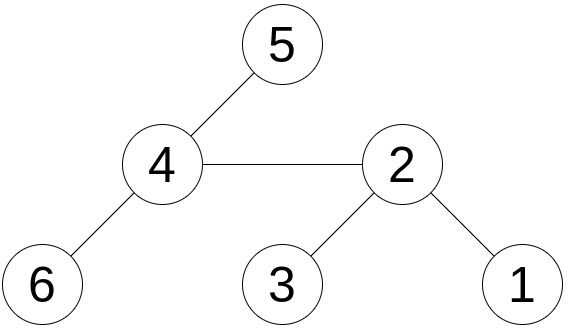
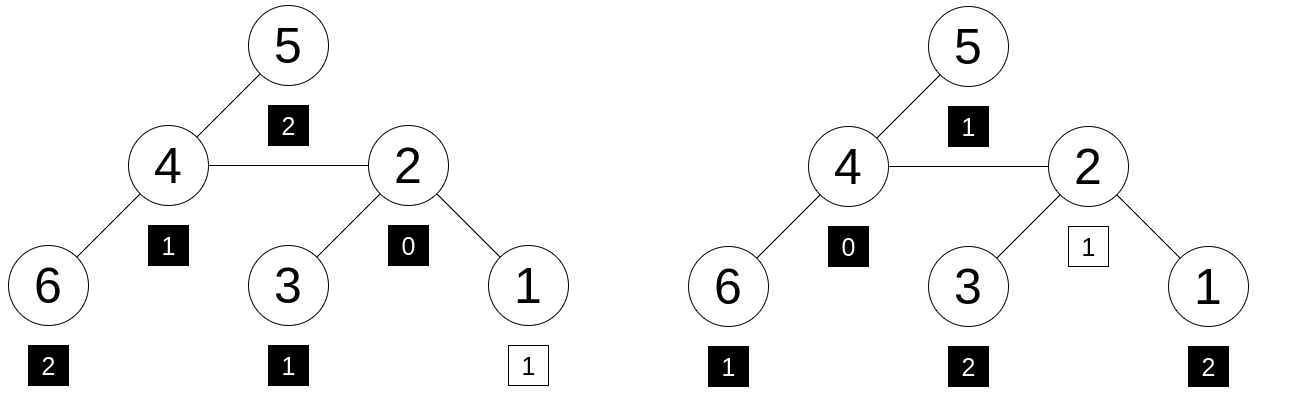
下图是样例一中的树。  下图是两种树的编码方法，故点 $2$（参见左图）、点 $4$ （参见右图）是『好点』。图中矩形表示每个点的标记。 黑色矩形中包含了给定列表中的所有数字，而唯一的一个白色矩形中包含了唯一一个未出现在给定列表中的数字。  样例二中的唯一『好点』是点 $3$，样例三中没有『好点』。