CF1795D Triangle Coloring

给定一个无向图，该图包含 $n$ 个顶点和 $n$ 条边，其中 $n$ 能被 $6$ 整除。每条边都有一个权值，是一个正整数（大于零）。 该图具有如下结构：它被分成 $\frac{n}{3}$ 个三元组，每个三元组由连续的三个顶点组成，第一个三元组为顶点 $1, 2, 3$，第二个三元组为顶点 $4, 5, 6$，以此类推。每个三元组内的任意两个顶点之间都有一条边。不同三元组之间没有边相连。 你需要将该图的所有顶点染成红色或蓝色，每个顶点恰好染一种颜色，且红色顶点和蓝色顶点的数量都为 $\frac{n}{2}$。如果满足这些条件，则称该染色方案是合法的。 一个染色方案的权值定义为：所有连接着颜色不同的两个顶点的边的权值之和。 设 $W$ 为所有合法染色方案中可能取得的最大权值。请计算有多少种合法染色方案的权值等于 $W$，并将结果对 $998244353$ 取模后输出。

第一行包含一个整数 $n$（$6 \le n \le 3 \cdot 10^5$，$n$ 能被 $6$ 整除）。 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$（$1 \le w_i \le 1000$），表示每条边的权值。第 $1$ 条边连接顶点 $1$ 和 $2$，第 $2$ 条边连接顶点 $1$ 和 $3$，第 $3$ 条边连接顶点 $2$ 和 $3$，第 $4$ 条边连接顶点 $4$ 和 $5$，第 $5$ 条边连接顶点 $4$ 和 $6$，第 $6$ 条边连接顶点 $5$ 和 $6$，以此类推。

输出一个整数，表示权值等于最大值 $W$ 的合法染色方案数，对 $998244353$ 取模。

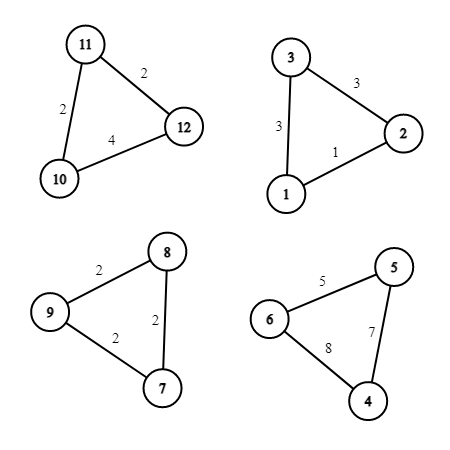
下图描述了第一个样例测试中的图结构。  该图的最大权值合法染色方案的权值为 $31$。 由 ChatGPT 4.1 翻译