CF1797A Li Hua and Maze

There is a rectangular maze of size $ n\times m $ . Denote $ (r,c) $ as the cell on the $ r $ -th row from the top and the $ c $ -th column from the left. Two cells are adjacent if they share an edge. A path is a sequence of adjacent empty cells. Each cell is initially empty. Li Hua can choose some cells (except $ (x_1, y_1) $ and $ (x_2, y_2) $ ) and place an obstacle in each of them. He wants to know the minimum number of obstacles needed to be placed so that there isn't a path from $ (x_1, y_1) $ to $ (x_2, y_2) $ . Suppose you were Li Hua, please solve this problem.

The first line contains the single integer $ t $ ( $ 1 \le t \le 500 $ ) — the number of test cases. The first line of each test case contains two integers $ n,m $ ( $ 4\le n,m\le 10^9 $ ) — the size of the maze. The second line of each test case contains four integers $ x_1,y_1,x_2,y_2 $ ( $ 1\le x_1,x_2\le n, 1\le y_1,y_2\le m $ ) — the coordinates of the start and the end. It is guaranteed that $ |x_1-x_2|+|y_1-y_2|\ge 2 $ .

For each test case print the minimum number of obstacles you need to put on the field so that there is no path from $ (x_1, y_1) $ to $ (x_2, y_2) $ .

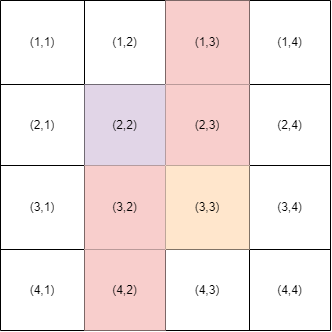
In test case 1, you can put obstacles on $ (1,3), (2,3), (3,2), (4,2) $ . Then the path from $ (2,2) $ to $ (3,3) $ will not exist.