CF1797A Li Hua and Maze

有一个大小为 $n\times m$ 的矩形迷宫。用 $(r,c)$ 表示从上到下第 $r$ 行、从左到右第 $c$ 列的格子。如果两个格子有公共边，则称它们是相邻的。路径是由一系列相邻的空格子组成的序列。 每个格子初始时都是空的。李华可以选择一些格子（除了 $(x_1, y_1)$ 和 $(x_2, y_2)$），并在每个格子上放置一个障碍物。他想知道，最少需要放置多少个障碍物，才能使得从 $(x_1, y_1)$ 到 $(x_2, y_2)$ 不存在路径。 假如你是李华，请解决这个问题。

第一行包含一个整数 $t$（$1 \le t \le 500$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n, m$（$4 \le n, m \le 10^9$），表示迷宫的大小。 每个测试用例的第二行包含四个整数 $x_1, y_1, x_2, y_2$（$1 \le x_1, x_2 \le n, 1 \le y_1, y_2 \le m$），表示起点和终点的坐标。 保证 $|x_1-x_2|+|y_1-y_2| \ge 2$。

对于每个测试用例，输出一个整数，表示你需要在迷宫中放置的最少障碍物数量，使得从 $(x_1, y_1)$ 到 $(x_2, y_2)$ 不存在路径。

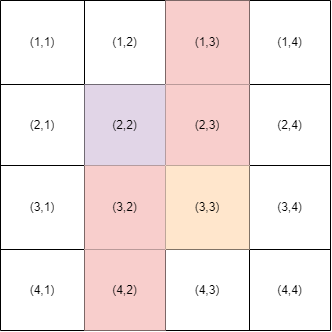
在第 1 个测试用例中，你可以在 $(1,3), (2,3), (3,2), (4,2)$ 这四个位置放置障碍物。这样从 $(2,2)$ 到 $(3,3)$ 的路径就不存在了。  由 ChatGPT 4.1 翻译