CF1797D Li Hua and Tree

李华有一棵包含 $n$ 个结点和 $n-1$ 条边的树。树的根为结点 $1$。每个结点 $i$ 有一个重要性 $a_i$。子树的大小定义为其包含的结点数，子树的总重要性为其所有结点的重要性之和。对于非叶子结点，其重儿子定义为子树大小最大的儿子；若有多个，则选择编号最小的那个作为重儿子。 李华需要进行 $m$ 次操作： - “1 $x$” ($1\leq x\leq n$) —— 计算以 $x$ 为根的子树的重要性。 - “2 $x$” ($2\leq x\leq n$) —— 将 $x$ 的重儿子旋转到上方。具体来说，设 $son_x$ 为 $x$ 的重儿子，$fa_x$ 为 $x$ 的父亲。操作为删除 $x$ 与 $fa_x$ 之间的边，并连接 $son_x$ 与 $fa_x$。保证 $x$ 不是根结点，但不保证 $x$ 不是叶子结点。如果 $x$ 是叶子结点，则忽略该操作。 假如你是李华，请解决这个问题。

第一行包含两个整数 $n,m$（$2\le n\le 10^{5},1\le m\le 10^{5}$）——树的结点数和操作数。 第二行包含 $n$ 个整数 $a_{1},a_{2},\ldots ,a_{n}$（$-10^{9}\le a_{i}\le 10^{9}$）——每个结点的重要性。 接下来 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1\le u_i,v_i\le n$，$u_i\ne v_i$）——表示一条树边。给定的边构成一棵树。 接下来 $m$ 行，每行一个操作。第 $j$ 行包含两个整数 $t_{j},x_{j}$（$t_{j}\in \{1,2\}$，$1 \leq x_{j} \leq n$，若 $t_j = 2$，则 $x_{j}\neq 1$）——表示第 $j$ 次操作。

对于每个“1 $x$”操作，输出一行答案。

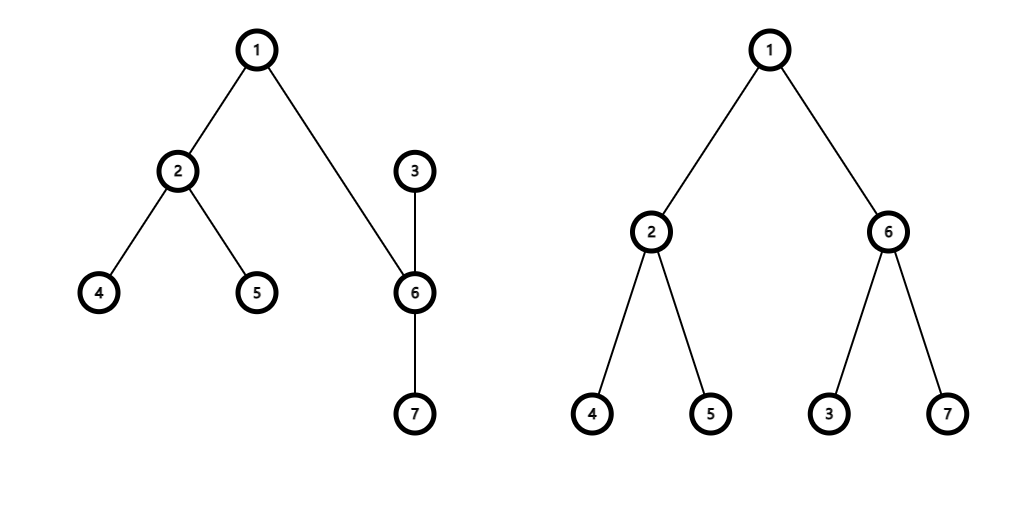
在第一个样例中： 初始树如下图所示：  结点 $6$ 的子树重要性为 $a_6+a_7=2$。 将结点 $3$ 的重儿子（即 $6$）旋转到上方后，树结构如下图所示：  此时结点 $6$ 的子树重要性为 $a_6+a_3+a_7=3$。 结点 $2$ 的子树重要性为 $a_2+a_4+a_5=3$。 由 ChatGPT 4.1 翻译