CF1797F Li Hua and Path

李华有一棵包含 $n$ 个顶点和 $n-1$ 条边的树。顶点编号从 $1$ 到 $n$。 对于一对顶点 $(u,v)$（$u < v$），如果下列两个陈述中恰好有一个为真，则称这对顶点是“可爱对”： - $u$ 是路径 $(u,v)$ 上所有顶点中编号最小的顶点。 - $v$ 是路径 $(u,v)$ 上所有顶点中编号最大的顶点。 接下来有 $m$ 次操作。每次操作，他会选择一个整数 $k_j$，然后将编号为 $n+j$ 的新顶点插入到树中，并与编号为 $k_j$ 的顶点连接。 他想要计算在操作前以及每次操作后树中“可爱对”的数量。 假设你就是李华，请解决这个问题。

第一行包含一个整数 $n$（$2\le n\le 2\cdot 10^5$）——树的顶点数。 接下来的 $n-1$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1\le u_i,v_i\le n$，$u_i\ne v_i$）——表示一条树边。所给边保证构成一棵树。 接下来一行包含一个整数 $m$（$1\le m\le 2\cdot 10^5$）——操作次数。 接下来的 $m$ 行，每行一个整数 $k_j$（$1\le k_j < n+j$）——表示每次操作连接的顶点编号。

输出 $m+1$ 个整数，分别表示操作前以及每次操作后树中“可爱对”的数量。

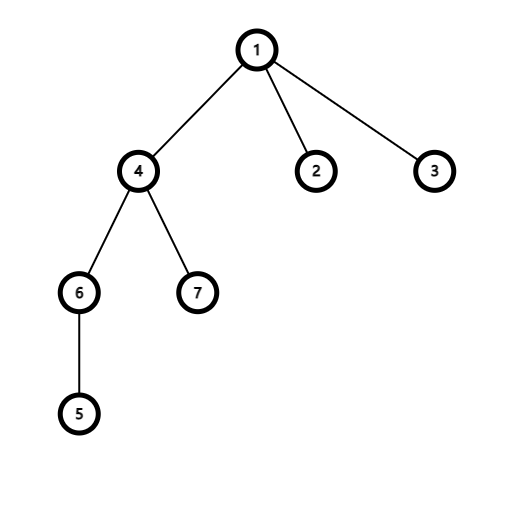
初始树如下图所示：  共有 $11$ 个“可爱对”——$(1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)$。 同理，可以计算每次操作后的“可爱对”数量，结果分别为 $15$ 和 $19$。 由 ChatGPT 4.1 翻译