CF1798C Candy Store

商店里有 $n$ 种糖果，编号从 $1$ 到 $n$。第 $i$ 种糖果的单价为 $b_i$ 个硬币，商店里共有 $a_i$ 个第 $i$ 种糖果。 你需要将所有糖果分装成若干包，每包只能包含一种糖果。形式化地说，对于每种糖果 $i$，你需要选择一个整数 $d_i$，表示每包第 $i$ 种糖果的数量，要求 $a_i$ 能被 $d_i$ 整除。 那么，每包第 $i$ 种糖果的价格为 $b_i \cdot d_i$。我们记这个价格为 $c_i$，即 $c_i = b_i \cdot d_i$。 包装完成后，这些糖果包会被放在货架上。考虑货架上这些糖果包的价格，依次为 $c_1, c_2, \ldots, c_n$。价格标签用于标注糖果包的价格。一个价格标签可以标注从第 $l$ 包到第 $r$ 包（包含两端），如果 $c_l = c_{l+1} = \ldots = c_r$。每一包糖果都必须被至少一个价格标签标注。例如，如果 $c_1, \ldots, c_n = [4, 4, 2, 4, 4]$，那么只需 $3$ 个价格标签：第一个标签标注第 $1,2$ 包，第二个标签标注第 $3$ 包，第三个标签标注第 $4,5$ 包。 给定整数 $a_1, b_1, a_2, b_2, \ldots, a_n, b_n$。你的任务是选择整数 $d_i$，使得 $a_i$ 能被 $d_i$ 整除，且使得标注所有糖果包价格所需的价格标签数量最小。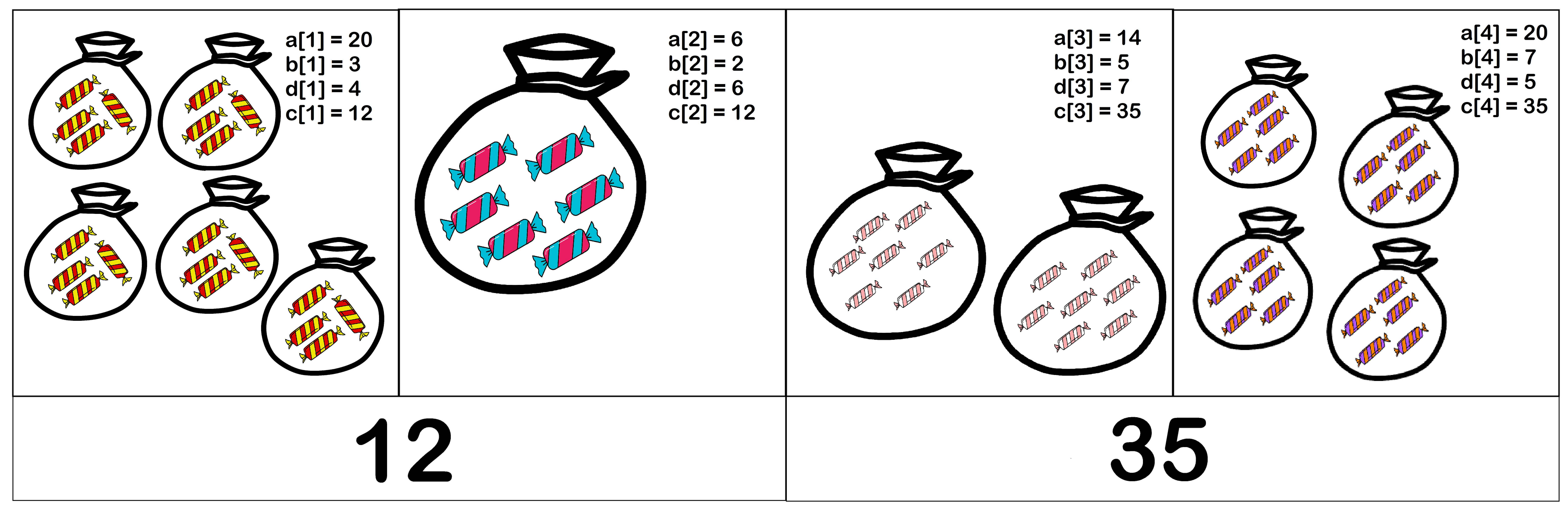 为了更好地理解题意，请参考第一组测试样例的插图：  我们再重复一下题目中用到的符号的含义： $a_i$ —— 商店中第 $i$ 种糖果的数量。 $b_i$ —— 第 $i$ 种糖果的单价。 $d_i$ —— 每包第 $i$ 种糖果的数量。 $c_i$ —— 每包第 $i$ 种糖果的价格，计算公式为 $c_i = b_i \cdot d_i$。

每组测试数据包含多组测试用例。第一行包含一个整数 $t$（$1 \le t \le 100\,000$），表示测试用例的组数。接下来是每组测试用例的描述。 每组测试用例的第一行包含一个整数 $n$（$2 \le n \le 200\,000$），表示糖果的种类数。 接下来每组测试用例的 $n$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i \le 10^9$，$1 \le b_i \le 10\,000$），分别表示第 $i$ 种糖果的数量和单价。 保证所有测试用例中 $n$ 的总和不超过 $200\,000$。

对于每组测试用例，输出一个整数，表示标注所有糖果包价格所需的最小价格标签数量。

在第一个测试用例中，你可以选择 $d_1 = 4$，$d_2 = 6$，$d_3 = 7$，$d_4 = 5$。此时各包的价格为 $[12, 12, 35, 35]$。只需 $2$ 个价格标签，分别标注 $c_1, c_2$ 和 $c_3, c_4$。可以证明，无论如何选择 $d_i$，至少需要 $2$ 个价格标签来标注所有糖果包。此例在题面插图中也有展示。 在第二个测试用例中，选择 $d_1 = 4$，$d_2 = 2$，$d_3 = 10$，所有糖果包的价格均为 $20$。因此只需 $1$ 个价格标签。注意所有 $a_i$ 都能被 $d_i$ 整除，这是必须满足的条件。 在第三个测试用例中，不难发现可以用一个价格标签标注第 $2,3,4$ 包，另外分别为第 $1$ 包和第 $5$ 包各用一个价格标签。共需 $3$ 个价格标签。 由 ChatGPT 4.1 翻译