CF1805C Place for a Selfie

宇宙是一个坐标平面。有 $n$ 条太空高速公路，每条高速公路都是一条经过原点 $(0, 0)$ 的直线 $y=kx$。此外，平面上还有 $m$ 条小行星带，我们将其表示为开口向上的抛物线，即函数 $y=ax^2+bx+c$ 的图像，其中 $a>0$。 你想要为每条抛物线拍照。为此，对于每条抛物线，你需要选择一条既不与该抛物线相交，也不与其相切的直线。对于不同的抛物线，你可以选择同一条直线。请为每条抛物线找到这样一条直线，或者判断不存在这样的直线。

每个测试点包含多组测试用例。第一行包含测试用例数 $t$（$1 \le t \le 10^4$）。接下来是每个测试用例的描述。 每个测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \le n, m \le 10^5$），分别表示直线和抛物线的数量。 接下来的 $n$ 行，每行包含一个整数 $k$（$|k| \le 10^8$），表示一条直线 $y=kx$ 的系数。直线不一定互不相同，$k$ 可以等于 $0$。 接下来的 $m$ 行，每行包含三个整数 $a$、$b$ 和 $c$（$a, |b|, |c| \le 10^8$，且 $a>0$），表示抛物线 $y=ax^2+bx+c$ 的系数。抛物线不一定互不相同。 保证所有测试用例中 $n$ 的总和不超过 $10^5$，$m$ 的总和也不超过 $10^5$。

对于每个测试用例，按给定顺序输出每条抛物线的答案。如果存在一条既不与该抛物线相交也不与其相切的直线，则输出一行 "YES"，下一行输出该直线的系数 $k$。如果有多种答案，输出任意一种均可。如果不存在这样的直线，输出一行 "NO"。 输出答案时大小写均可。例如，"yEs"、"yes"、"Yes" 和 "YES" 都会被识别为肯定回答。 输出示例中的空行仅用于说明，你可以输出也可以不输出。

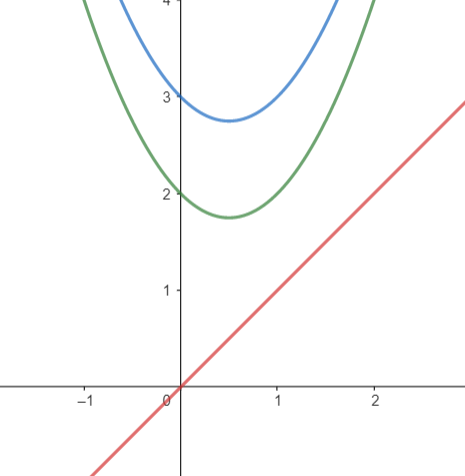
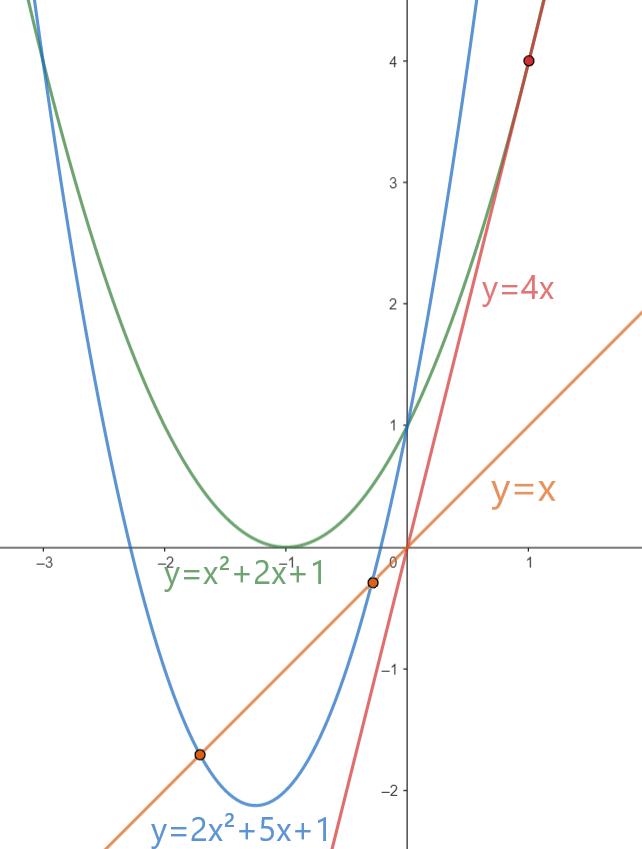
在第一个测试用例中，两条抛物线都不与唯一的一条直线 $y=1\cdot x$ 相交，因此答案都是 $1$。  在第二个测试用例中，直线 $y=x$ 与抛物线 $2x^2+5x+1$ 相交，直线 $y=4x$ 与抛物线 $x^2+2x+1$ 相切，因此这些配对都不满足条件。所以对于第一条抛物线，答案是 $1$（$y=1x$），对于第二条抛物线，答案是 $4$。  在第三组测试数据中，直线与抛物线相交，因此答案为 "NO"。 由 ChatGPT 4.1 翻译