CF1805E There Should Be a Lot of Maximums

给定一棵树（一种无环连通图）。树的每个顶点上都有一个整数。我们定义树的 $\mathrm{MAD}$（最大重复数）参数为：在树的所有顶点中，出现次数至少为 $2$ 的最大整数。如果树中没有任何数出现超过一次，则认为 $\mathrm{MAD}=0$。 注意，如果你从树中删除一条边，树会被分成两棵子树。我们分别计算这两棵子树的 $\mathrm{MAD}$ 参数，并取两者中的较大值。这个结果就是被删除的那条边的值。 对于每条边，求出其对应的值。注意，实际上并不需要真的删除任何边，每条边的值是独立计算的。

第一行包含一个整数 $n$（$2 \le n \le 10^5$），表示树的顶点数。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$），表示树中的一条边。保证给出的边构成一棵合法的树。 最后一行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le 10^9$），表示每个顶点上的数。

对于每条边，按照输入顺序输出一个数，表示删除该边后得到的两棵子树的 $\mathrm{MAD}$ 参数的最大值。

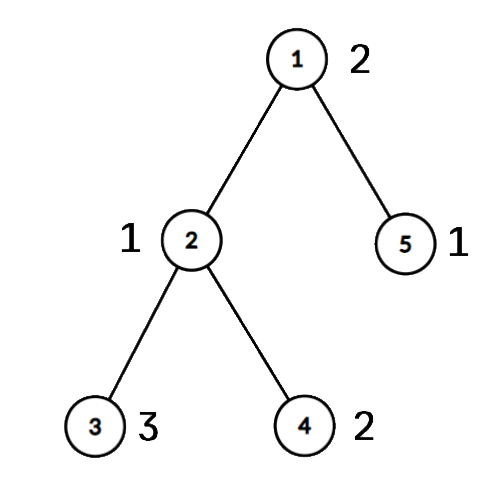
 在第一个样例中，删除边 $(1, 2)$ 后，任意一棵子树中都没有数出现 $2$ 次，因此答案为 $\max(0, 0)=0$。 删除边 $(2, 3)$ 后，在较大的子树中，$1$ 出现了两次，$2$ 也出现了两次，因此这棵树的 $\mathrm{MAD}$ 为 $2$。 删除边 $(2, 4)$ 后，在较大的子树中，只有 $1$ 出现了两次，另一棵子树中只有一个数，因此答案为 $1$。 在第二个样例中，如果不删除边 $1 \leftrightarrow 4$，那么其中一棵子树会有两个 $1$，所以答案为 $1$。如果删除边 $1 \leftrightarrow 4$，两棵子树都没有重复的数，因此答案为 $0$。 由 ChatGPT 4.1 翻译