CF1810F M-tree

一棵有根树被称为“好树”，如果树中的每个结点要么是叶子结点（即没有子结点的结点），要么恰好有 $m$ 个子结点。 对于一棵好树，每个叶子结点 $u$ 上写有一个正整数 $c_u$，我们定义该叶子的值为 $c_u + \mathrm{dep}_u$，其中 $\mathrm{dep}_u$ 表示从结点 $u$ 到根结点的路径上的边数（也称为 $u$ 的深度）。一棵好树的值定义为所有叶子结点值的最大值。 现在，给定一个长度为 $n$ 的整数数组 $a_1, a_2, \ldots, a_n$，这些整数需要写在叶子结点上。你需要构造一棵有 $n$ 个叶子的好树，并将数组 $a$ 中的整数写到所有叶子结点上。形式化地说，你需要为每个叶子结点 $u$ 分配一个下标 $b_u$，其中 $b$ 是一个长度为 $n$ 的排列，表示写在叶子 $u$ 上的整数为 $c_u = a_{b_u}$。在这些约束下，你需要最小化好树的值。 你有 $q$ 个询问。每个询问给定 $x$ 和 $y$，将 $a_x$ 改为 $y$，之后你需要输出基于当前数组 $a$ 的最小好树值。 长度为 $n$ 的排列是一个包含 $1$ 到 $n$ 的 $n$ 个互不相同整数的数组，顺序任意。例如，$[2,3,1,5,4]$ 是一个排列，但 $[1,2,2]$ 不是排列（$2$ 在数组中出现了两次），$[1,3,4]$ 也不是排列（$n=3$ 但数组中有 $4$）。

每个测试点包含多组测试数据。第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的组数。接下来是每组测试数据的描述。 每组测试数据的第一行包含三个整数 $n$、$m$ 和 $q$（$1\le n,q \le 2 \times 10^5$，$2\le m \le 2\times 10^5$，$n \equiv 1 \pmod{m-1}$），分别表示叶子结点数、常数 $m$ 和询问数。 第二行包含 $n$ 个整数 $a_1,a_2,\ldots,a_n$（$1 \le a_i \le n$），表示初始数组。 接下来的 $q$ 行，每行包含两个整数 $x$ 和 $y$（$1\le x,y\le n$），表示将 $a_x$ 改为 $y$ 的一次询问。 保证所有测试用例中 $n$ 的总和与 $q$ 的总和不超过 $2\times 10^5$。

对于每组测试数据，输出 $q$ 个整数，按顺序输出每次修改后的最小好树值，所有结果输出在一行，用空格隔开。

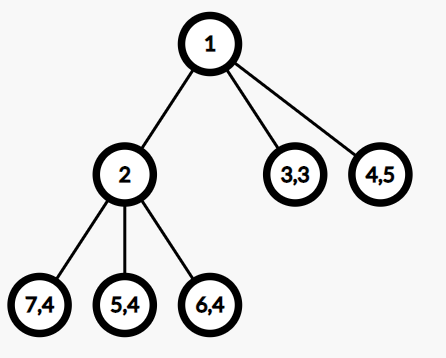
在第一个测试用例中，第一次询问后，当前数组 $a$ 为 $[4,3,4,4,5]$。我们可以构造如下的好树：  每个结点内的第一个数字是其编号（本题中编号无关紧要，仅用于帮助理解）。如果结点是叶子，结点内的第二个数字是写在其上的整数。 可以看出，$\mathrm{dep}_3=\mathrm{dep}_4=1,\mathrm{dep}_5=\mathrm{dep}_6=\mathrm{dep}_7=2$，树的值（所有叶子的最大值）为 $5+1=6$。叶子 $5$、$6$、$7$ 的值也等于 $6$。可以证明，这棵树的值在所有合法树中是最小的。 由 ChatGPT 4.1 翻译