CF1810F M-tree

A rooted tree is called good if every vertex of the tree either is a leaf (a vertex with no children) or has exactly $ m $ children. For a good tree, each leaf $ u $ has a positive integer $ c_{u} $ written on it, and we define the value of the leaf as $ c_{u} + \mathrm{dep}_{u} $ , where $ \mathrm{dep}_{u} $ represents the number of edges of the path from vertex $ u $ to the root (also known as the depth of $ u $ ). The value of a good tree is the maximum value of all its leaves. Now, you are given an array of $ n $ integers $ a_{1}, a_{2}, \ldots, a_{n} $ , which are the integers that should be written on the leaves. You need to construct a good tree with $ n $ leaves and write the integers from the array $ a $ to all the leaves. Formally, you should assign each leaf $ u $ an index $ b_{u} $ , where $ b $ is a permutation of length $ n $ , and represent that the integer written on leaf $ u $ is $ c_u = a_{b_{u}} $ . Under these constraints, you need to minimize the value of the good tree. You have $ q $ queries. Each query gives you $ x $ , $ y $ and changes $ a_{x} $ to $ y $ , and after that, you should output the minimum value of a good tree based on the current array $ a $ . A permutation of length $ n $ is an array consisting of $ n $ distinct integers from $ 1 $ to $ n $ in arbitrary order. For example, $ [2,3,1,5,4] $ is a permutation, but $ [1,2,2] $ is not a permutation ( $ 2 $ appears twice in the array), and $ [1,3,4] $ is also not a permutation ( $ n=3 $ but there is $ 4 $ in the array).

Each test contains multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Their description follows. The first line contains three integers $ n $ , $ m $ , and $ q $ ( $ 1\le n,q \le 2 \cdot 10^5 $ , $ 2\le m \le 2\cdot 10^5 $ , $ n \equiv 1 \pmod {m - 1} $ ) — the number of the leaves, the constant $ m $ , and the number of queries. The second line contains $ n $ integers $ a_{1},a_{2}, \ldots, a_{n} $ ( $ 1 \le a_{i} \le n $ ) — the initial array. For the following $ q $ lines, each line contains two integers $ x $ and $ y $ ( $ 1\le x,y\le n $ ), representing a query changing $ a_{x} $ to $ y $ . It is guaranteed that both the sum of $ n $ and the sum of $ q $ do not exceed $ 2\cdot 10^5 $ .

For each test case, output $ q $ integers in one line, the $ i $ -th of which is the minimum tree value after the $ i $ -th change.

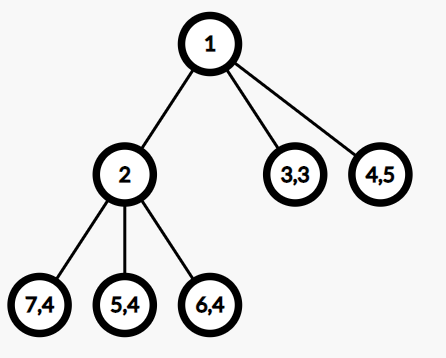In the first test case, after the first query, the current array $ a $ is $ [4,3,4,4,5] $ . We can construct such a good tree: The first number inside a vertex is its index (in this problem, the indices do not matter, but help to understand the figure). If a vertex is a leaf, the second number inside the vertex is the integer written on it. We can tell that $ \mathrm{dep}_{3}=\mathrm{dep}_{4}=1,\mathrm{dep}_{5}=\mathrm{dep}_{6}=\mathrm{dep}_{7}=2 $ and the value of the tree, which is the maximum value over all leaves, is $ 5+1=6 $ . The value of leaves $ 5 $ , $ 6 $ , $ 7 $ is also equal to $ 6 $ . It can be shown that this tree has the minimum value over all valid trees.