CF1811B Conveyor Belts

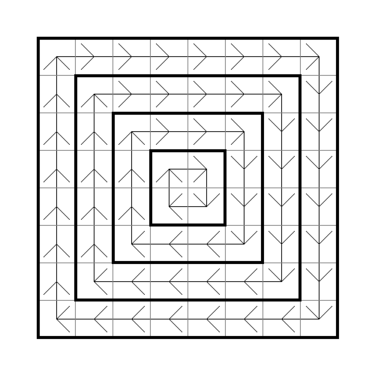
传送带矩阵 $m_n$ 是一个 $n \times n$ 的矩阵，其中 $n$ 是一个偶数。该矩阵由若干同心的“带”组成，每一圈带都按顺时针方向移动。 换句话说，当 $n=2$ 时，传送带矩阵就是一个 $2 \times 2$ 的矩阵，其所有格子构成一个长度为 $4$ 的顺时针环路。对于任意自然数 $k \ge 2$，矩阵 $m_{2k}$ 是通过在矩阵 $m_{2k-2}$ 的外围添加一圈顺时针环路得到的。  如图所示为 $8 \times 8$ 的传送带矩阵。你现在站在坐标为 $x_1, y_1$ 的格子上，想要到达坐标为 $x_2, y_2$ 的格子。如果某个格子位于第 $x$ 行第 $y$ 列，则其坐标为 $x, y$。 你每秒会自动沿着所在带的顺时针方向移动到下一个格子。你也可以随时花费 $1$ 单位能量移动到相邻的格子（上下左右），这种移动是瞬时完成的，且你可以在任意时刻进行任意多次。 你的任务是计算，从坐标为 $x_1, y_1$ 的格子到坐标为 $x_2, y_2$ 的格子，所需花费的最小能量。 例如，对于 $n=8$，你初始在坐标 $1,3$，目标是到达坐标 $6,4$。你可以立即进行 $2$ 次能量移动，来到坐标 $3,3$，然后等待 $8$ 秒后即可到达目标格子。

第一行包含一个整数 $t$（$1 \le t \le 2 \times 10^5$），表示测试用例的数量。 接下来是每个测试用例的描述。 每个测试用例包含一行，包含五个整数 $n$、$x_1$、$y_1$、$x_2$、$y_2$（$1 \le x_1, y_1, x_2, y_2 \le n \le 10^9$），分别表示矩阵的大小、起点和终点的坐标。保证 $n$ 为偶数。

对于每个测试用例，输出一行一个整数，表示从坐标 $x_1, y_1$ 到坐标 $x_2, y_2$ 所需花费的最小能量。

由 ChatGPT 4.1 翻译