CF1819C The Fox and the Complete Tree Traversal

给定整数 $n$ 和一棵包含 $n$ 个节点的树。 记 $\text{Dist}(x,y)$ 表示树上节点 $x,y$ 之间最短路径的边数。 你需要判断是否存在一个 $1\sim n$ 的排列 $p$，满足： - $\text{Dist}(p_i,p_{i+1})\leq 2$ 对任意整数 $i(1\leq i

第一行输入一个整数 $n(2\leq n\leq2\times10^5)$。 接下来输入 $n-1$ 行，每行输入两个整数 $u,v(1\leq u,v\leq n;u\not=v)$，表示树的节点 $u,v$ 之间有一条边。 保证给定的是棵树。

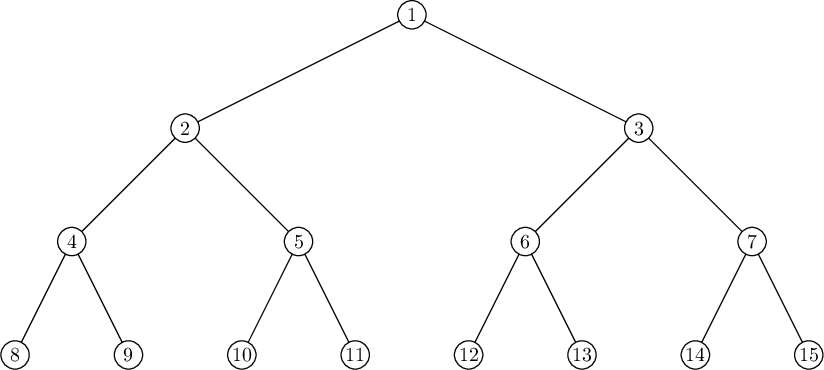
对于每组数据： 如果不存在满足要求的 $p$，输出一行 `No`。 否则： - 首先输出一行 `Yes`。 - 接下来输出一行 $n$ 个整数表示你所构造的满足要求的排列 $p$。 如果有多个满足要求的 $p$，输出任意一个即可。 ### 样例解释 下方的图片分别展示了样例一和样例三对应的树。

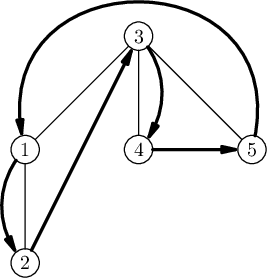The tree from the first example is shown below. The bold arrows indicate the fox's route. In the second example, any sequence of three different vertices is a correct route, because the fox can jump from any vertex to any vertex. The tree from the third example is shown below. It can be shown that there is no required route for it.